
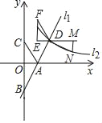
����Ŀ����ͼ��ֱ������ϵxOy�У�ֱ��11��y��tx��t��t��0���ֱ���x�ᡢy�ύ��A��B���㣬��˫����l2��y��![]() ��k��0�����ڵ�D��2��2������B��C����x��Գƣ�����AC����Rt��AOC��AD����ƽ�ƣ�ʹ��A�ƶ�����D���õ�Rt��DEF��
��k��0�����ڵ�D��2��2������B��C����x��Գƣ�����AC����Rt��AOC��AD����ƽ�ƣ�ʹ��A�ƶ�����D���õ�Rt��DEF��
��1��д��k��ֵ����A�����ꣻ
��2����F�Ƿ���l2�ϣ�����֤��Ľ��ۣ�
��3����ED���ӳ�����ȡһ��M��4��2��������M��MN��y�ᣬ��l2�ڵ�N������ND����ֱ��ND�Ľ���ʽ��
��4��ֱ��д���߶�ACɨ���������
���𰸡���1��k��4��A��1��0������2����F��l2�ϣ���3��y����![]() x+3����4���߶�ACɨ�����������ƽ���ı���ACFD�������4��
x+3����4���߶�ACɨ�����������ƽ���ı���ACFD�������4��
��������
��1�����ô���ϵ������x���ϵ�������������ɵó����ۣ�
��2����ȷ������B�����꣬�����ó���C�����꣬����ƽ�������F�����꣬�жϼ��ɣ�
��3����ȷ������N�����꣬���ô���ϵ�������ɵó����ۣ�
��4�����жϳ�ACɨ���IJ�����ƽ���ı���ACFD�����жϳ���C��D��E��һ��ֱ���ϣ�A��E��FҲ��ͬһ��ֱ���ϣ����ɽ��ۣ�
��1���ߵ�D��2��2����˫����l2��y��![]() ��k��0���ϣ�
��k��0���ϣ�
��2��![]() ��
��
��k��4
��D��2��2����ֱ��11��y��tx��t��t��0���ϣ�
��2t��t��2��
��t��2��
��ֱ��11��y��2x��2
��y��0��
��2x��2��0��
��x��1��
��A��1��0����
�ʴ�Ϊ��4����1��0����
��2����F��l2�ϣ�
�ɣ�1��֪��ֱ��l1��y��2x��2��
���B��0����2����
�ߵ�B��C����x��Գƣ�
��C��0��2����
��ƽ�ƺ�DE��AO��1��EF��CO��2��
���E��1��2������F��1��4��
��˫����l2�Ľ���ʽΪ��y��![]() ��
��
���F��1��4���������������ʽy��![]() ���ʵ�F��l2�ϣ�
���ʵ�F��l2�ϣ�
��3����M��4��2����MN��y�ᣬ��l2�ڵ�N��
���N�ĺ��������4������y��![]() �ϣ�
�ϣ�
��N��4��1����
��D��2��2����
��ֱ��ND�Ľ���ʽΪy��ax+b������a��bΪ��������a��0����
��![]() �����
����� ��
��
��ֱ��ND�Ľ���ʽΪ��y����![]() x+3��
x+3��
��4����ͼ������CF��CE��AE��
��ƽ��֪��ACɨ���IJ�����ƽ���ı���ACFD��
�ɣ�1��֪��C��0��2����E��1��2����
��D��2��2����
���C��D��E��һ��ֱ���ϣ�
ͬ��A��E��FҲ��ͬһ��ֱ���ϣ�
��ƽ��֪��EF��DE��
��F��1��4����
��AF��4��
��CD��2��
���߶�ACɨ�����������ƽ���ı���ACFD�������![]() ��CD��AF��4��
��CD��AF��4��


 �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��b��c�dz�����a��0��ͼ���һ���֣���x��Ľ���A�ڵ㣨2��0���ͣ�3��0��֮�䣬�Գ�����x=1����������˵������ab��0����2a+b=0����3a+c��0����a+b��m��am+b����mΪʵ������������1��x��3ʱ��y��0��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ���õ���A���ɶ��������ӵĴ�ϸ����ϸ����ɵ���U����װ����ע��һ������ˮ��ˮ��߶�Ϊ6cm���ֽ��ұ�ϸ����A��˳ʱ����ת60����ABλ�ã������ϸ��λ�ò��䣬���ʱ��U����װ�����ϸ����ˮ���ĸ߶�ԼΪ��������
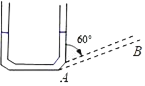
A. 4cmB. 2![]() cmC. 3cmD. 8cm
cmC. 3cmD. 8cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
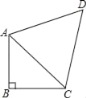
����Ŀ����ͼ����ABC��90����![]() ��BC��6��AD��DC����ADC��60����
��BC��6��AD��DC����ADC��60����
��1����AC����
��2������ADC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵxOy�У���������l��y����![]() x2+bx+c��b��cΪ�������Ķ���Dλ��ֱ��y����2��x��֮�����������ֱ��y����2��x�ᣩ����l��ֱ��y����1����ĸ����ǣ�������
x2+bx+c��b��cΪ�������Ķ���Dλ��ֱ��y����2��x��֮�����������ֱ��y����2��x�ᣩ����l��ֱ��y����1����ĸ����ǣ�������
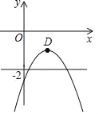
A. 0��B. 1����2��
C. 0����1����2��D. ֻ��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
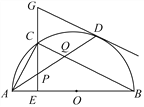
����Ŀ����ͼ���ڡ�O�У�AB��ֱ������D�ǡ�O��һ�㣬��C��![]() ���е㣬CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ����н�����ȷ����________(ֻ����д���)��
���е㣬CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ����н�����ȷ����________(ֻ����д���)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
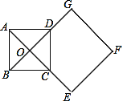
����Ŀ����ͼ��������ABCD�ĶԽ����ཻ�ڵ�O��������OEFG��һ��OG������D����D��OG���е㣬OG��![]() AB����������ABCD�̶�����������OEFG��O����ʱ����ת���ǣ���0��������360�����õ�������OE��F��G����������__��ʱ����OAG����90����
AB����������ABCD�̶�����������OEFG��O����ʱ����ת���ǣ���0��������360�����õ�������OE��F��G����������__��ʱ����OAG����90����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����|m+3|+![]() ��0����P��m��n������x��ĶԳƵ�P��Ϊ���κ���ͼ�㣬����κ����Ľ���ʽΪ��������
��0����P��m��n������x��ĶԳƵ�P��Ϊ���κ���ͼ�㣬����κ����Ľ���ʽΪ��������
A. y��![]() ��x��3��2+2B. y��
��x��3��2+2B. y��![]() ��x+3��2��2
��x+3��2��2
C. y��![]() ��x��3��2��2D. y��
��x��3��2��2D. y��![]() ��x+3��2+2
��x+3��2+2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڼ��ڣ�С���С�������ȥ���Σ������ھ��㿴��һ�ù�������С�쾪�ȵ�˵����ѽ���������ߣ���60���ף���С��ȴ����ΪȻ����60���ף��ҿ�û�У������������۲��ݣ��ְ�Ц��˵���������ˣ������Ҵ���һ�����ǰ壬������ѧ����֪ʶ��һ������һ�㣬��˭˵�Ķɣ���
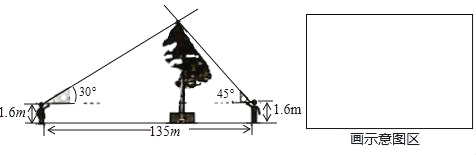
С���С�����������²�������ͼ��ʾ��С���С���ֱ������Ķ�������ͬһ��ƽ���ϣ���������ƽ�����ǰ壬�������ǰ��һ��ֱ�DZ����ƽ��ƽ�У�Ȼ��ǰ���ƶ�����λ�ã�ʹĿ���������ǰ��б�����þ���������ߵ㣬��ʱ�����С���С��֮��ľ���Ϊ135�ף����ǵ��۾�������ľ��붼��1.6�ף�
��1������ָ�������ڻ���С���С�������������ߵ�ʾ��ͼ��
��2��ͨ������˵��С���С��˭��˵����ȷ����������ȷ��0.1�����ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.24��
��2.24��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com