
【题目】某工厂设门市部专卖某产品,该产品每件成本40元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
每件销售价(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
每天售出件数 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设当天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察这些统计数据,找出每天售出件数y与每件售价x(元)之间的函数关系,并写出该函数关系式.
(2)门市部原设有两名营业员,但当销售量较大时,在每天售出量超过168件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为40元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)
【答案】
(1)解:经过图表数据分析,每天售出件数y与每件售价x(元)之间的函数关系为一次函数,
设y=kx+b,经过(50,300)、(60,240),
![]() ,
,
解得k=﹣6,b=600,
故y=﹣6x+600
(2)解:①设每件产品应定价x元,由题意列出函数关系式
W=(x﹣40)×(﹣6x+600)﹣3×40
=﹣6x2+840x﹣24000﹣120
=﹣6(x2﹣140x+4020)
=﹣6(x﹣70)2+5280.
②当y=168时x=72,这时只需要两名员工,
W=(72﹣40)×168﹣80=5296>5280.
故当每件产品应定价72元,才能使每天门市部纯利润最大
【解析】(1)经过图表数据分析,每天售出件数y与每件售价x(元)之间的函数关系为一次函数,设y=kx+b,解出k、b即可求出;(2)由利润=(售价﹣成本)×售出件数﹣工资,列出函数关系式,求出最大值.


科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AD⊥BC于点D,以AD为一边向右作等边三角形ADE,DE与AC交于点F.
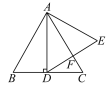
(1)试判断DF与EF的数量关系,并给出证明;
(2)若CF的长为2 cm,试求等边三角形ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( ) 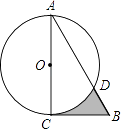
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为(3,﹣2),线段AB的位置如图所示,其中点A的坐标为(7,3),点B的坐标为(1,4).
(1)将线段AB平移可以得到线段MN,其中点A的对应点为M(3,﹣2),点B的对应点为N,则点N的坐标为 .
(2)在(1)的条件下,若点C的坐标为(4,0),请在图中描出点N并顺次连接BC,CM,MN,NB,然后求出四边形BCMN的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为 .
的图象上,则k的值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com