Question

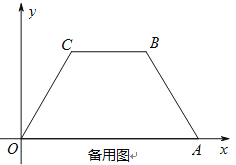
【题目】如图，在平面直角坐标系中，四边形OABC是等腰梯形，BC∥OA，OA=7，AB=4，∠ COA=60°，点P为x轴上的—个动点，点P不与点O、点A重合．连结CP，过点P作PD交AB于点D．

（1）求点B的坐标；

（2）当点P运动什么位置时，△OCP为等腰三角形，求这时点P的坐标；

（3）当点P运动什么位置时，使得∠CPD=∠OAB，且=，求这时点P的坐标。

Answer 1

【答案】（1）B（5， ）；（2）P（4，0）或P（-4，0）；（3）P（1，0）或P（6，0）

【解析】解：（1）过C作CM⊥x轴，垂足M，过B作BN⊥x轴，垂足N

因为四边形OABC是等腰梯形，AB=4, ∠COA=60°

故：OC=AB=4，∠OAB=60°，AN=OM，CM=BN

故：OM=1/2OC=2=AN，CM=2√3=BN

因为BC//OA,OA=7

故：MN=OA-OM-AN=3

故：ON=OM+MN=5

故：B（5，2√3）

（2）如果△OCP为等腰三角形，因为∠COA=60°

则：△OCP为正三角形或P在x轴的负半轴上

①当△OCP为正三角形时

故：OP=OC=4

故：P（4，0）

②P在x轴的负半轴上时

也有OP=OC=4

故：P（-4，0）

（3）∠CPD=∠OAB=∠COA =60°

故：∠OPC+∠DPA=∠DPA+∠ADP=120°

故：∠OPC=∠ADP

故：△OPC∽△ADP

故：OP/AD=OC/PA

因为8*BD=5*AB, AB=4

故：BD=5/2

故：AD=AB-BD=3/2

设OP =x，故：PA=OA-OP=7-x

故：x/(3/2)=4/(7-x)

故：x=1或x=6

故：P（1，0）或P（6，0）