
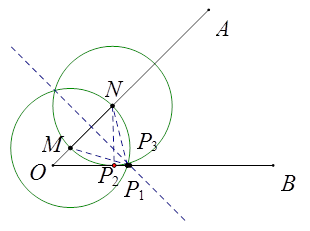
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.
【答案】x=0或x= ![]() 或4≤x<4
或4≤x<4 ![]()
【解析】解:以MN为底边时,可作MN的垂直平分线,与OB必有一个交点P1 , 且MN=4,以M为圆心MN为半径画圆,以N为圆心MN为半径画圆,
①如下图,当M与点O重合时,即x=0时,
除了P1 , 当MN=MP,即为P3;当NP=MN时,即为P2;
只有3个点P;
②当0<x<4时,如下图,圆N与OB相切时,NP2=MN=4,且NP2⊥OB,此时MP3=4,
则OM=ON-MN= ![]() NP2-4=
NP2-4= ![]() .
.
③因为MN=4,所以当x>0时,MN<ON,则MN=NP不存在,
除了P1外,当MP=MN=4时,
过点M作MD⊥OB于D,当OM=MP=4时,圆M与OB刚好交OB两点P2和P3;
当MD=MN=4时,圆M与OB只有一个交点,此时OM= ![]() MD=4
MD=4 ![]() ,
,
故4≤x<4 ![]() .
.
与OB有两个交点P2和P3 ,
所以答案是x=0或x= ![]() 或4≤x<4
或4≤x<4 ![]() .
.
【考点精析】掌握相交两圆的性质是解答本题的根本,需要知道相交的两个圆的连心线垂直平分两圆的公共弦.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某兴趣小组用仪器测测量湛江海湾大桥主塔的高度.如图,在距主塔从AE60米的D处.用仪器测得主塔顶部A的仰角为68°,已知测量仪器的高CD=1.3米,求主塔AE的高度(结果精确到0.1米)
(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某县政府为了迎接“八一”建军节,加强军民共建活动,计划从花园里拿出1430盆甲种花卉和1220盆乙种花卉,搭配成A、B两种园艺造型共20个,在城区内摆放,以增加节日气氛,已知搭配A、B两种园艺造型各需甲、乙两种花卉数如表所示:(单位:盆)
(1)某校某年级一班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮忙设计出来.
(2)如果搭配及摆放一个A造型需要的人力是8人次,搭配及摆放一个B造型需要的人力是11人次,哪种方案使用人力的总人次数最少,请说明理由.
造型 | A | B |
甲种 | 80 | 50 |
乙种 | 40 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
七年级兴趣班报名情况统计表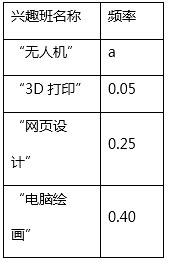
(1)报名参加兴趣班的总人数为人;统计表中的a=;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)
(1)求∠BCD的度数.
(2)求教学楼的高BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径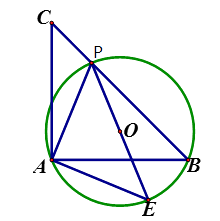
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0).将矩形OABC绕点O按顺时针方向旋转135°,得到矩形EFGH(点E与O重合).
(1)若GH交y轴于点M,则∠FOM=°,OM=;
(2)将矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFGH与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤4 ![]() ﹣2时,S与t之间的函数关系式.
﹣2时,S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在弧BD上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.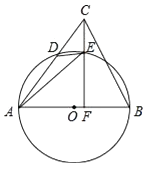
(1)求证:CF⊥AB;
(2)若CD=4,CB=4 ![]() ,cos∠ACF=
,cos∠ACF= ![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com