
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足是G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,则EF的长是 . 
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D. 
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
A.乙到达B地时甲距A地120km.
B.乙出发1.8小时被甲追上.
C.甲,乙相距20km时,t为2.4h.
D.甲的速度是乙的速度的 ![]() 倍.
倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求A、B两种钢笔每支各多少元?
(2)若该文具店要购进A,B两种钢笔共90支,总费用不超过1588元,并且A种钢笔的数量少于B种钢笔的数量,那么该文具店有哪几种购买方案?
(3)文具店以每支30元的价格销售B种钢笔,很快销售一空,于是,文具店决定在进价不变的基础上再购进一批B种钢笔,涨价卖出,经统计,B种钢笔售价为30元时,每月可卖68支;每涨价1元,每月将少卖4支,设文具店将新购进的B种钢笔每支涨价a元(a为正整数),销售这批钢笔每月获利W元,试求W与a之间的函数关系式,并且求出B种铅笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是第39个植树节,我们提出了“追求绿色时尚,走向绿色文明”的倡议.某校为积极响应这一倡议,立即在八、九年级开展征文活动,校团委对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图. 
(1)求扇形统计图中投稿3篇的班级个数所对应的扇形的圆心角的度数.
(2)求该校八、九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数最多的4个班中,八、九年级各有两个班,校团委准备从这四个班中选出两个班参加全校的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)求线段CD的长;
(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.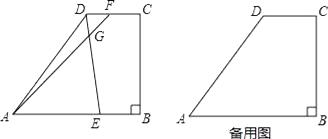
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com