
【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在弧BD上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.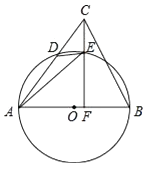
(1)求证:CF⊥AB;
(2)若CD=4,CB=4 ![]() ,cos∠ACF=
,cos∠ACF= ![]() ,求EF的长.
,求EF的长.
【答案】
(1)
证明:连接BD,
∵AB是⊙O的直径,∴∠ADB=90°,∴∠DAB+∠1=90°,
∵∠1=∠2,∠2=∠3,∴∠1=∠3,∴∠DAB+∠3=90°,
∴∠CFA=180°﹣(DAB+∠3)=90°,∴CF⊥AB;
(2)
解:连接OE,
∵∠ADB=90°,∴∠CDB=180°﹣∠ADB=90°,
∵在Rt△CDB中,CD=4,CB=4 ![]() ,
,
∴DB= ![]() ,
,
∵∠1=∠3,∴cos∠1=cos∠3= ![]() ,∴AB=10,
,∴AB=10,
∴OA=OE=5,AD= ![]() ,
,
∵CD=4,∴AC=AD+CD=10,
∵CF=ACcos∠3=8,∴AF= ![]() ,
,
∴OF=AF﹣OA=1,∴EF= ![]() .
.
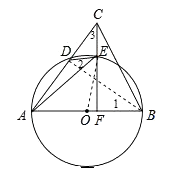
【解析】(1)连接BD,由AB是圆O的直径,得到∠ADB=90°,根据余角的性质得到∠CFA=180°-(∠DAB+∠3)=90°,于是得到结论;
(2)连接OE,由∠ADB=90°,得到∠CDB=180°-∠ADB=90°,根据勾股定理得到DB=![]() =8,解直角三角形得到CD=4,根据勾股定理即可得到结论。
=8,解直角三角形得到CD=4,根据勾股定理即可得到结论。
【考点精析】解答此题的关键在于理解余角和补角的特征的相关知识,掌握互余、互补是指两个角的数量关系,与两个角的位置无关,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(﹣3,1),B(0,3),C(0,1) 
(1)将△ABC以点O为旋转中心顺时针旋转90°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1 , BA1后,求四边形ABA1B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含l0千克)的种子,超过l0千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
①一次购买种子数量不超过l0千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过l0千克的那部分种子的价格打五折:
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是( ).
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)求线段CD的长;
(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.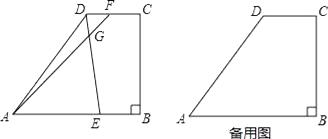
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣3,0)和点B,与y轴交于点C(0,3),顶点为点D,对称轴DE交x轴于点E,连接AD,AC,DC.
(1)求抛物线的函数表达式.
(2)判断△ADC的形状,并说明理由.
(3)对称轴DE上是否存在点P,使点P到直线AD的距离与到x轴的距离相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com