
【题目】梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含l0千克)的种子,超过l0千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
①一次购买种子数量不超过l0千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过l0千克的那部分种子的价格打五折:
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是( ).
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:①由图可知,一次购买种子数量不超过10千克时,销售价格为:50÷10=5元/千克,正确; ②由图可知,超过10千克的那部分种子的价格为:(150-50)÷(50-10)=2.5元/千克,所以,一次购买30千克种子时,付款金额为:50+2.5×(30-10)=100元,正确; ③由于一次购买10千克以上种子时,超过10千克的那部分种子的价格为2.5元/千克,而2.5÷5=0.5,所以打五折,正确; ④由于一次购买40千克种子需要:50+2.5×(40-10)=125元, 分两次购买且每次购买20千克种子需要:2×[50+2.5×(20-10)]=150元, 而150-125=25元, 所以一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱,正确. 故选D.
【考点精析】认真审题,首先需要了解一次函数的概念(一般地,如果y=kx+b(k,b是常数,k不等于0),那么y叫做x的一次函数),还要掌握一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径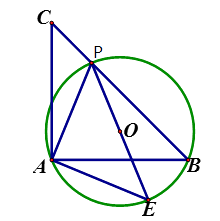
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)b= , c= , 点B的坐标为;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在弧BD上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.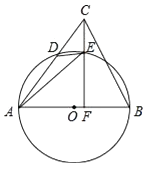
(1)求证:CF⊥AB;
(2)若CD=4,CB=4 ![]() ,cos∠ACF=
,cos∠ACF= ![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅家的阳台上放置了一个晒衣架如图1,图2是晒衣架的侧面示意图,A,B两点立于地面,将晒衣架稳固张开,测得张角∠AOB=62°,立杆OA=OB=140cm,小梅的连衣裙穿在衣架后的总长度为122cm,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(GPick,1859~1942年)证明了格点多边形的面积公式S=a+ ![]() b﹣1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+
b﹣1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+ ![]() ×6﹣1=6
×6﹣1=6
(1)请在图中画一个格点正方形,使它的内部只含有4个格点,并写出它的面积.
(2)请在图乙中画一个格点三角形,使它的面积为 ![]() ,且每条边上除顶点外无其它格点.(注:图甲、图乙在答题纸上)
,且每条边上除顶点外无其它格点.(注:图甲、图乙在答题纸上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上. 
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com