
【题目】如图,△ABC是等边三角形,过AB边上的点D作GD∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD; 
(1)求证:△ADG是等边三角形;
(2)求证:△AGE≌△DAC;
(3)过点E作EF∥DC,交BC于点F,连接AF,求∠AEF的度数.
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC,
又∵GD∥BC,
∴∠ADG=∠ACB=∠ABC=60°,
∴△ADG是等边三角形;
(2)证明:∵△ADG是等边三角形,
∴∠DAG=∠ADG=∠AGD=60°,AD=AG=DG,
又∵DE=DB,
∵DE+DG=DB+AD,
即EG=AB,
又∵AB=AC,
∴EG=AC,
在△AGE和△DAC中
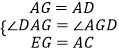
∴△AGE≌△DAC(SAS);
(3)解:∵△AGE≌△DAC,
∴∠AEG=∠ACD,
又∵EF∥DC,GD∥BC,
∴∠DCB=∠EFB,∠EFB=∠FEG,
∴∠DCB=∠FEG,
∴∠AEF=∠AEG+∠FEG=∠ACD+∠DCB=∠ACB=60°.
【解析】(1)利用已知条件和等边三角形的性质可证明∠ADG=∠ACB=∠ABC=60°,进而可证明△ADG是等边三角形;(2)易证AG=AD,EG=AC,由全等三角形的判定方法SAS即可证明△AGE≌△DAC;(3)结合(2)可得∠AEF=∠AEG+∠FEG=∠ACD+∠DCB=∠ACB=60°.
【考点精析】认真审题,首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)已知二次函数y=x2-2x-3,请你化成y=(x-h)2+k的形式为____________,并在直角坐标系中画出y=x2-2x-3的图象;
(2)如果A(x1,y1),B(x2,y2)是(1)中图象上的两点,且x1<x2<1,请直接写出y1、y2的大小关系为___________;
(3)利用(1)中的图象表示出方程x2-2x-1=0的根来,要求保留画图痕迹,说明解题思路即可,不用计算结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(2﹣3x)(x+1)
(2)[5xy2(x2﹣3xy)﹣(﹣x2y2)3]÷(5xy)
(3)(x+2)2(x﹣2)2(x2+4)2
(4)(x+y﹣z)(x﹣y+z)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,BD为高.(从下列问题中任选一问作答) 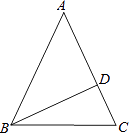
(1)若∠ABD+∠C=120°,求∠A的度数;
(2)若CD=3,BC=5,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形OEFG中,点A和点F的坐标分别为 (3,2),(-1,-1),则两个正方形的位似中心的坐标是( )

A.(1,0)
B.(-5,-1)
C.(1,0)或(-5,-1)
D.(1,0)或(-5,-2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com