
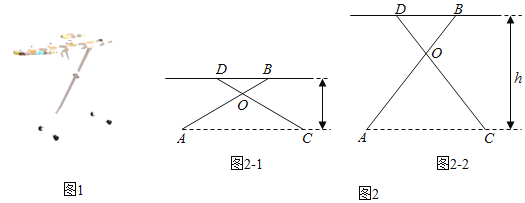
【题目】有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到lcm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,
,![]() ,与坐标轴交于A、B两点.
,与坐标轴交于A、B两点.
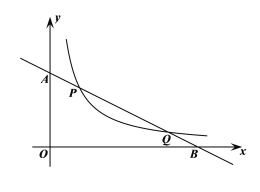
(1)求一次函数与反比例函数的解析式;
(2)观察图象,当![]() 时,直接写出不等式
时,直接写出不等式![]() 的解集;
的解集;
(3)将直线![]() 向下平移
向下平移![]() 个单位,若直线与反比例函数
个单位,若直线与反比例函数![]() 的图象有唯一交点,求
的图象有唯一交点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
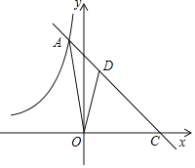
【题目】如图,在平面直角坐标系xOy中,函数y=﹣x+5的图象与函数y=![]() (k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求k的值;
(2)根据图象,直接写出当x<0时不等式![]() >﹣x+5的解集;
>﹣x+5的解集;
(3)求△AOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
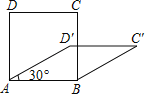
【题目】四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
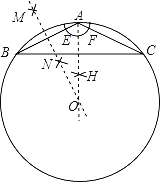
【题目】如图,在等腰△ABC中,AB=AC=2![]() ,BC=8,按下列步骤作图:
,BC=8,按下列步骤作图:
①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于![]() EF的长为半径作弧相交于点H,作射线AH;
EF的长为半径作弧相交于点H,作射线AH;
②分别以点A,B为圆心,大于![]() AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;
AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;
③以点O为圆心,线段OA长为半径作圆.
则⊙O的半径为( )
A.2![]() B.10C.4D.5
B.10C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
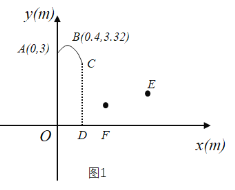
【题目】在篮球比赛中,东东投出的球在点A处反弹,反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系),抛物线顶点为点B.
(1)求该抛物线的函数表达式.
(2)当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m.
①求OD的长.
②东东抢到球后,因遭对方防守无法投篮,他在点D处垂直起跳传球,想将球沿直线快速传给队友华华,目标为华华的接球点E(4,1.3).东东起跳后所持球离地面高度h1(m)(传球前)与东东起跳后时间t(s)满足函数关系式h1=﹣2(t﹣0.5)2+2.7(0≤t≤1);小戴在点F(1.5,0)处拦截,他比东东晚0.3s垂直起跳,其拦截高度h2(m)与东东起跳后时间t(s)的函数关系如图2所示(其中两条抛物线的形状相同).东东的直线传球能否越过小戴的拦截传到点E?若能,东东应在起跳后什么时间范围内传球?若不能,请说明理由(直线传球过程中球运动时间忽略不计).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形![]() 绕点
绕点![]() 顺时针旋转得到矩形
顺时针旋转得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]()
(1)当点![]() 落在
落在![]() 上时
上时
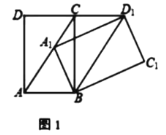
①如图1,若![]() ,求证:
,求证:![]()
②如图2,![]() 交
交![]() 于点
于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
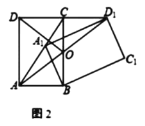
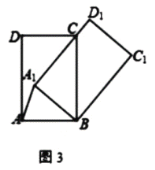
(2)若![]() ,
,
①如图3,当![]() 过点C时,则
过点C时,则![]() 的长=_____.
的长=_____.
②当![]() 时,作
时,作![]() ,
,![]() 绕点
绕点![]() 转动,当直线
转动,当直线![]() 经过
经过![]() 时,直线
时,直线![]() 交边
交边![]() 于
于![]() ,
,![]() 的值=______.
的值=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
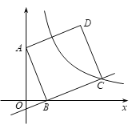
【题目】如图,在直角坐标系中,正方形ABCD绕点A(0,6)旋转,当点B落在x轴上时,点C刚好落在反比例函数![]() (k≠0,x>0)的图像上.已知sin∠OAB=
(k≠0,x>0)的图像上.已知sin∠OAB=![]() .
.
(1)求反比例函数的表达式;
(2)反比例函数![]() 的图像是否经过AD边的中点,并说明理由.
的图像是否经过AD边的中点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com