
【题目】将矩形![]() 绕点
绕点![]() 顺时针旋转得到矩形
顺时针旋转得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]()
(1)当点![]() 落在
落在![]() 上时
上时
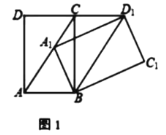
①如图1,若![]() ,求证:
,求证:![]()
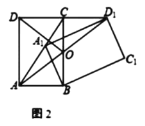
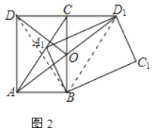
②如图2,![]() 交
交![]() 于点
于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,
,
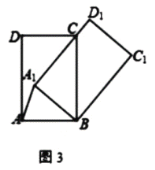
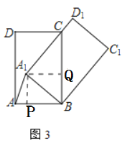
①如图3,当![]() 过点C时,则
过点C时,则![]() 的长=_____.
的长=_____.
②当![]() 时,作
时,作![]() ,
,![]() 绕点
绕点![]() 转动,当直线
转动,当直线![]() 经过
经过![]() 时,直线
时,直线![]() 交边
交边![]() 于
于![]() ,
,![]() 的值=______.
的值=______.
【答案】(1)①见解析,②见解析;(2)①![]() ,②
,②![]()
【解析】
(1)①首先证明△A1B是等边三角形,可得∠AA1B=∠A1BD1=60°,即可解决问题.
②首先证明Rt△BCD1≌RtD1A1B(HL),得到四边形ABD1C是平行四边形,推出OC=OB,再证明△DCO≌△ABO(SAS)即可解决问题.
(2)①如图3中,作A1E⊥AB于E,A1F⊥BC于F.利用勾股定理求出AE,A1E即可解决问题;
②分两种情况,当△A1BE旋转到图4位置时以及当△A1BE旋转到图5位置时,分别证明△DAN∽△BEN即利用相似比得到![]() .
.
(1)证明:①∵∠CAB=60°,
由旋转可知,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=∠CAB =60°,
∴∠AA1B=∠A1BD1,![]() ;
;
②如图2中,连接BD1,BD,DD1.
由旋转可知:BA=BA1,BD=BD1,∠ABA1=∠DBD1,
∴∠BAA1=∠BDD1,
∵在矩形ABCD中,∠BAA1=∠ABD=∠BDC,
∴∠BDC=∠BDD1,
∴D,C,D1共线,
∵∠BCD1=∠BA1D1=90°,
∴在中Rt△BCD1与RtD1A1B中
BD1=D1B,BC=A1D1,
∴Rt△BCD1≌RtD1A1B(HL),
∴CD1=BA1,
∵BA=BA1,
∴AB=CD1,
∵AC=BD1
∴四边形ABD1C是平行四边形,
∴OC=OB
∵CD=BA,∠DCO=∠ABO=90°,
∴△DCO≌△ABO(SAS),
∴DO=OA.
(2)①如图3中,作A1P⊥AB于P,A1Q⊥BC于Q.
在Rt△A1BC中,∵∠CA1B=90°,BC=15.A1B=CD=9,
∴CA1=![]() ,
,
∵![]() ,
,
∴A1Q=![]() ,
,
∵∠A1QB=∠A1PB=∠PBQ=90°,
∴四边形A1PBQ是矩形,
∴PB=A1Q=![]() ,A1P=BQ=
,A1P=BQ=![]() ,
,
∴AP=9![]() =
=![]() ,
,
在Rt△AA1E中,AA1=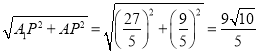 ,
,
故答案为:![]()
②当△A1BE旋转到图4位置时,直线A1E经过点D,
由旋转可知,A1B=AB=9,
∵∠A1BE=45°,∠A1EB=90°,
∴BE=A1E=![]() ,
,
∵∠A1EB=∠DAN=90°,∠AND=∠ENB,
∴△AND∽△ENB,
∴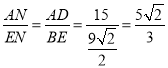 ,
,
当△A1BE旋转到图5位置时,直线A1E经过点D,
由旋转可知,A1B=AB=9,
∵∠A1BE=45°,∠A1EB=90°,
∴BE=A1E=![]() ,
,
∵∠DAN=∠BEN=90°,∠AND=∠ENB,
∴△DAN∽△BEN,
∴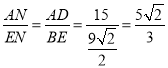 ,
,
综上所述,![]() ,
,
故答案为:![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
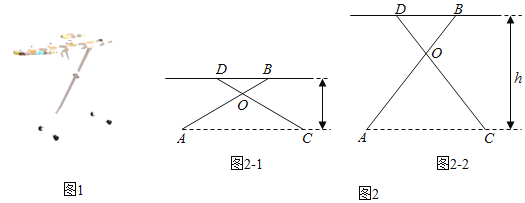
【题目】有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到lcm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
查看答案和解析>>
科目:初中数学 来源: 题型:
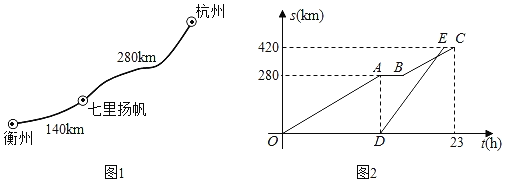
【题目】2020年5月16日,“钱塘江诗路”航道全线开通,一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h,游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变).
(1)写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.
(2)若货轮比游轮早36分钟到达衢州.问:
①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?
查看答案和解析>>
科目:初中数学 来源: 题型:
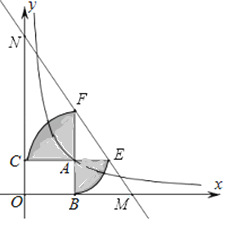
【题目】如图,已知动点A在函数![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校举行“经典诵读”比赛,诵读材料有:A《唐诗》、B《宋词》、C《论语》.将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小红和小亮参加诵读比赛,比赛时小红先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行比赛.
(1)小红诵读《论语》的概率是 ;
(2)请用列表法或画树状图的方法,求小红和小亮诵读两个相同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成圆形阴影.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为( )
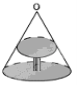
A.0.36πm2B.0.81πm2C.1.44πm2D.3.24πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
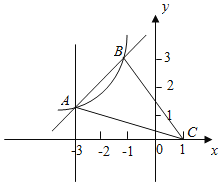
【题目】如图,在平面立角坐标系中,反比例函数y=![]() (k≠0,x<0)与一次函数y=ax+b的图象交于点A(﹣3,1)、B(m,3).点C的坐标为(1,0),连接AC,BC.
(k≠0,x<0)与一次函数y=ax+b的图象交于点A(﹣3,1)、B(m,3).点C的坐标为(1,0),连接AC,BC.
(1)求反比例函数和一次函数的表达式;
(2)当x<0时,直接写出不等式![]() ≥ax+b的解集 ;
≥ax+b的解集 ;
(3)若点M为y轴的正半轴上的动点,当△ACM是直角三角形时,直接写出点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
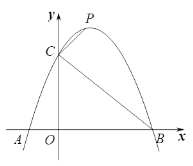
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com