
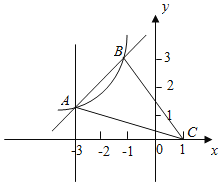
����Ŀ����ͼ����ƽ����������ϵ�У�����������y��![]() ��k��0��x��0����һ�κ���y��ax+b��ͼ���ڵ�A(��3��1)��B(m��3)����C������Ϊ(1��0)������AC��BC��
��k��0��x��0����һ�κ���y��ax+b��ͼ���ڵ�A(��3��1)��B(m��3)����C������Ϊ(1��0)������AC��BC��
��1������������һ�κ����ı���ʽ��
��2����x��0ʱ��ֱ��д������ʽ![]() ��ax+b�Ľ⼯�� ����
��ax+b�Ľ⼯�� ����
��3������MΪy����������ϵĶ��㣬����ACM��ֱ��������ʱ��ֱ��д����M�������� ����
���𰸡���1��y����![]() ��y��x+4����2����1��x��0��x����3����3��(0��13)��(0��
��y��x+4����2����1��x��0��x����3����3��(0��13)��(0��![]() )
)
��������
��1���ô���ϵ����������⣻
��2���۲캯��ͼ����⣻
��3����MC��б�ߡ�CA��б�ߡ�AM��б������������ֱ���⼴�ɣ�
�⣺��1������A��������뷴������������ʽ�ã�1��![]() ����ã�k����3��
����ã�k����3��
����B��������뷴������������ʽ����ã�m����1���ʵ�B����1��3����
����A��B���������һ�κ�������ʽ�ã� ![]() �����
�����![]() ��
��
�ʷ�����������һ�κ����ı���ʽ�ֱ�Ϊ��y����![]() ��y��x+4��
��y��x+4��
��2���۲캯��ͼ��ã���x��0ʱ��x����1��x����3ʱ������ʽ![]() ��ax+b������
��ax+b������
������ʽ�Ľ⼯Ϊ����1��x��0��x����3��
�ʴ�Ϊ����1��x��0��x����3��
��3�����M��0��m����m��0������C��1��0����A����3��1����
��MC2��1+m2��CA2����1+3��2+1��17��AM2��9+��m��1��2��
��MC��б��ʱ����1+m2��17+9+��m��1��2����ã�m��13��
��CA��б��ʱ��ͬ���ɵã�m��![]() ����ֵ����ȥ����
����ֵ����ȥ����
��AM��б��ʱ��ͬ���ɵã�m����4����ȥ����
�ʴ�Ϊ��0��13����0��![]() ����
����


 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�õ�����
˳ʱ����ת�õ�����![]() ����
����![]() �Ķ�Ӧ��ֱ�Ϊ
�Ķ�Ӧ��ֱ�Ϊ![]()
��1������![]() ����
����![]() ��ʱ
��ʱ
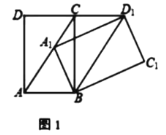
����ͼ1����![]() ����֤��
����֤��![]()
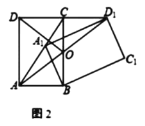
����ͼ2��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����֤��
����֤��![]() ��
��
��2����![]() ��
��
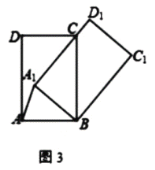
����ͼ3����![]() ����Cʱ����
����Cʱ����![]() �ij�=_____��
�ij�=_____��
�ڵ�![]() ʱ����
ʱ����![]() ��
��![]() �Ƶ�
�Ƶ�![]() ת������ֱ��
ת������ֱ��![]() ����
����![]() ʱ��ֱ��
ʱ��ֱ��![]() ����
����![]() ��
��![]() ��
��![]() ��ֵ=______��
��ֵ=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ijУ�ƻ���һ����״Ϊ���������ABC�Ŀյؽ�����̬�������죮��֪��ABC�ı�BC��120�ף���AD��80�ף�ѧУ�ƻ������ָ����AHG����BHE����GFC�;���EFGH�IJ��֣���ͼ�������о���EFGH��һ��EF�ڱ�BC�ϣ�������������H��G�ֱ��ڱ�AB��AC�ϣ��ּƻ�����AHG���ֲݣ�ÿƽ����Ͷ��6Ԫ������BHE����FCG�϶��ֻ���ÿƽ����Ͷ��10Ԫ���ھ���EFGH���˽�������أ�ÿƽ����Ͷ��4Ԫ��
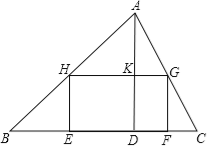
��1����FG��Ϊ������ʱ���ֲݵ�������ֻ��������ȣ�
��2��������EFGH�ı�FGΪ������ʱ����ABC�յظ�����Ͷ����С����СֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ĺ�����װ�����������һ��������Щ�����ɫ�ⶼ��ͬ��
��1�������������һ��������ɫ��Żأ��ٴ����������һ����
�������б�������״ͼ�������һ���������ڶ�����������ĸ��ʣ�
����ֱ��д�����������������ɫ�������ɫ�ĸ����� ����
��2�������������һ��������ɫ�Żأ��ٴ����������һ������ֱ��д�����������������ɫ�������ɫ�ĸ����� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҫ����ͼ����Ҫ��д��������Ҫ������ͼ�ۼ���
��1����ͼ1������ABCD�Ķ���A��D��Բ��, B��C������Բ�ڣ���֪Բ��O��������̶ȵ�ֱ����ͼ��������ֱ��l��AD��
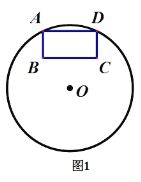
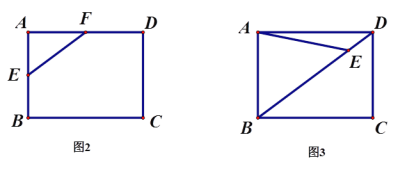
��2��������̶ȵ�ֱ��������ͼ2��ͼ3�а�Ҫ����ͼ������������ͼ�ζ�����ĸ��
��ͼ2�Ǿ���ABCD��E��F�ֱ���AB��AD���е㣬��EFΪ����һ�����Σ�
��ͼ3�Ǿ���ABCD��E�ǶԽ���BD������һ�㣨BE��DE������AEΪ����һ��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
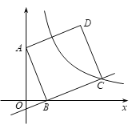
����Ŀ����ͼ����ֱ������ϵ�У�������ABCD�Ƶ�A��0��6����ת������B����x����ʱ����C�պ����ڷ���������![]() ��k��0��x��0)��ͼ���ϣ���֪sin��OAB��
��k��0��x��0)��ͼ���ϣ���֪sin��OAB��![]() .
.
��1�����������ı���ʽ��
��2������������![]() ��ͼ���Ƿ�AD�ߵ��е㣬��˵�����ɣ�
��ͼ���Ƿ�AD�ߵ��е㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
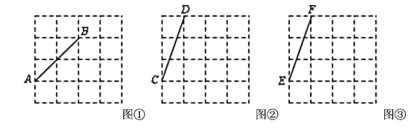
����Ŀ��ͼ�١�ͼ�ڡ�ͼ�۾���4��4������������ÿ��С�����εĶ����Ϊ��㣬С�����εı߳�Ϊ1����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ڸ���ϣ���ͼ�١�ͼ�ڡ�ͼ���У�ֻ���̶ȵ�ֱ�ߣ��ڸ����������а�Ҫ��ͼ������ͼ�εĶ�����ڸ���ϣ���Ҫ��д��������
���ڸ���ϣ���ͼ�١�ͼ�ڡ�ͼ���У�ֻ���̶ȵ�ֱ�ߣ��ڸ����������а�Ҫ��ͼ������ͼ�εĶ�����ڸ���ϣ���Ҫ��д��������
��1����ͼ�������߶�![]() Ϊ��һ��ֱ����
Ϊ��һ��ֱ����![]() ��
��
��2����ͼ�������߶�![]() Ϊ��һ����Գ���
Ϊ��һ����Գ���![]() ��ʹ�����Ϊ5��
��ʹ�����Ϊ5��
��3����ͼ�������߶�![]() Ϊ��һ����Գ��ı���
Ϊ��һ����Գ��ı���![]() ��ʹ�����Ϊ6��
��ʹ�����Ϊ6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ƶ�����ʤ֮�꣬����ij��Ϊ������ũ�����룬�������õ�������ɽ��������Դ��չ���̻�����������ҵ��ǰ������ũ��վ��������������������������������������������ĸ�Ʒ�ֹ�![]() �����������������ʵ�飬����ʵ�����ݻ��Ƴ���ͼ��ʾ������ͳ��ͼ�Ͳ�����������ͳ��ͼ����֪ʵ������صij�������
�����������������ʵ�飬����ʵ�����ݻ��Ƴ���ͼ��ʾ������ͳ��ͼ�Ͳ�����������ͳ��ͼ����֪ʵ������صij�������![]() ��
��
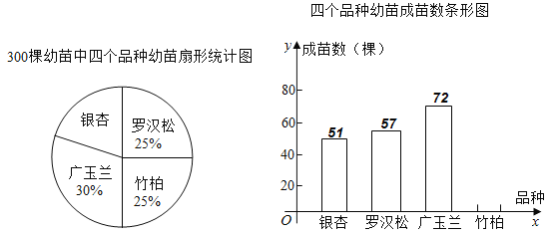
��1�����㲹ȫ����ͳ��ͼ��
��2���������![]() ��ʵ�������������ȡһ�����磬�����ܳ���ĸ��ʣ�
��ʵ�������������ȡһ�����磬�����ܳ���ĸ��ʣ�
��3�������г����飬���ĸ�Ʒ�ֵ������������ۡ������ۼۺ��г��������±���ʾ��
����Ʒ�� | ���� | ���� | ������ | ��� |
ÿ��������ۣ�Ԫ�� |
|
|
|
|
ÿ�ó����ۼۣ�Ԫ�� |
|
|
|
|
�г�������ã� |
|
|
|
|
������˹��������⣬����ÿ�ó��绹����ϵ�֧��![]() Ԫ��δ�ɹ������ɳ���Ĵ���֧�����Բ��ƣ�����������г�������֯
Ԫ��δ�ɹ������ɳ���Ĵ���֧�����Բ��ƣ�����������г�������֯![]() ��ũ����������������������粢��ȫ������������ɺ�Ϊ����
��ũ����������������������粢��ȫ������������ɺ�Ϊ����![]() ��ũ���������������Ԫ��
��ũ���������������Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com