
【题目】如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其余两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,每平方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元.
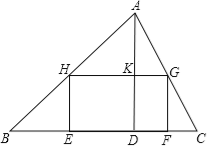
(1)当FG长为多少米时,种草的面积与种花的面积相等?
(2)当矩形EFGH的边FG为多少米时,△ABC空地改造总投资最小,最小值为多少?
【答案】(1)40;(2)FG=60时,△ABC空地改造总投资最小,最小值为26400.
【解析】
(1)可利用相似分别表示出相应的三角形的底与高,让面积相等即可;
(2)把相应的总投资用含x的代数式表示出后,求出二次函数的最值即可.
解:(1)设FG=x米,则AK=(80﹣x)米.
由△AHG∽△ABC,BC=120,AD=80,
可得:![]() ,
,
∴HG=![]() ,BE+FC=120﹣(
,BE+FC=120﹣(![]() )=
)=![]() ,
,
∴![]() ,
,
解得![]() .
.
∴当FG的长为40米时,种草的面积和种花的面积相等.
(2)设改造后的总投资为W元.
则W=![]()
=![]() ,
,
∵二次项系数6>0,0<x≤80,
∴当x=20时,W最小=26400.
答:当矩形EFGH的边FG长为20米时,空地改造的总投资最小,最小值为26400元.


科目:初中数学 来源: 题型:
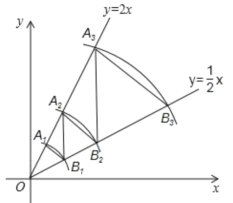
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 长为半径面弧,交直线
长为半径面弧,交直线![]() 于点
于点![]() ,…,按照如此规律进行下去,点
,…,按照如此规律进行下去,点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
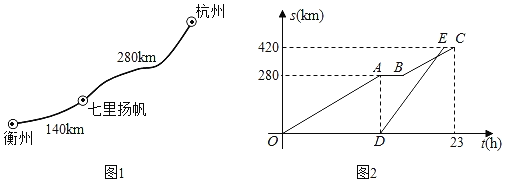
【题目】2020年5月16日,“钱塘江诗路”航道全线开通,一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h,游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变).
(1)写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.
(2)若货轮比游轮早36分钟到达衢州.问:
①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校举行“经典诵读”比赛,诵读材料有:A《唐诗》、B《宋词》、C《论语》.将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小红和小亮参加诵读比赛,比赛时小红先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行比赛.
(1)小红诵读《论语》的概率是 ;
(2)请用列表法或画树状图的方法,求小红和小亮诵读两个相同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成圆形阴影.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为( )
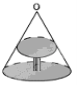
A.0.36πm2B.0.81πm2C.1.44πm2D.3.24πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组建了书法、音乐、美术、舞蹈、演讲5个社团,随机调查了部分学生.被调查学生每人都参加且只参加了其中一个社团活动,并将调查结果制成了如图两幅不完整的统计图,在扇形统计图中,“音乐”所对应的扇形圆心角度数是( )度.
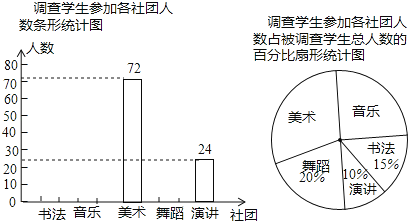
A.25%B.25C.60D.90
查看答案和解析>>
科目:初中数学 来源: 题型:
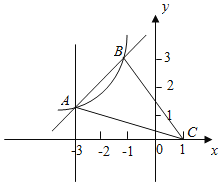
【题目】如图,在平面立角坐标系中,反比例函数y=![]() (k≠0,x<0)与一次函数y=ax+b的图象交于点A(﹣3,1)、B(m,3).点C的坐标为(1,0),连接AC,BC.
(k≠0,x<0)与一次函数y=ax+b的图象交于点A(﹣3,1)、B(m,3).点C的坐标为(1,0),连接AC,BC.
(1)求反比例函数和一次函数的表达式;
(2)当x<0时,直接写出不等式![]() ≥ax+b的解集 ;
≥ax+b的解集 ;
(3)若点M为y轴的正半轴上的动点,当△ACM是直角三角形时,直接写出点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点![]() 的横、纵坐标的绝对值之和叫做点
的横、纵坐标的绝对值之和叫做点![]() 的勾股值,记
的勾股值,记![]()
![]() .若抛物线
.若抛物线![]() 与直线
与直线![]() 只有一个交点
只有一个交点![]() ,已知点
,已知点![]() 在第一象限,且
在第一象限,且![]() ,令
,令![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
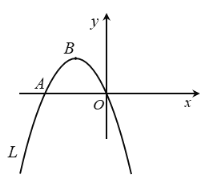
【题目】如图,抛物线![]()
![]() 经过原点和点
经过原点和点![]() ,顶点为
,顶点为![]() ,抛物线
,抛物线![]() 与抛物线
与抛物线![]() 关于原点
关于原点![]() 对称.
对称.
(1)求抛物线![]() 的函数表达式及点
的函数表达式及点![]() 的坐标;
的坐标;
(2)已知点![]() 、
、![]() 在抛物线
在抛物线![]() 上的对应点分别为
上的对应点分别为![]() 、
、![]() ,
,![]() 的对称轴交
的对称轴交![]() 轴于点
轴于点![]() ,则抛物线
,则抛物线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com