
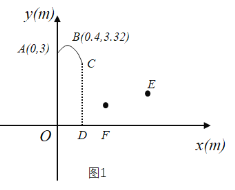
����Ŀ������������У�����Ͷ�������ڵ�A�����������������˶���·��Ϊ�����ߵ�һ���֣���ͼ1��ʾ����ֱ������ϵ���������߶���Ϊ��B��
��1����������ߵĺ�������ʽ��
��2�������˶�����Cʱ������������CD��x���ڵ�D��CD��2.6m��
����OD�ij���
�ڶ��������������Է�������Ͷ�������ڵ�D����ֱ���������뽫����ֱ�߿��ٴ������ѻ�����Ŀ��Ϊ�����Ľ����E��4��1.3�������������������������߶�h1��m��������ǰ���붫��������ʱ��t��s�����㺯����ϵʽh1����2��t��0.5��2+2.7��0��t��1����С���ڵ�F��1.5��0�������أ����ȶ�����0.3s��ֱ�����������ظ߶�h2��m���붫��������ʱ��t��s���ĺ�����ϵ��ͼ2��ʾ���������������ߵ���״��ͬ����������ֱ�ߴ����ܷ�Խ��С�������ش�����E�����ܣ�����Ӧ��������ʲôʱ�䷶Χ�ڴ��������ܣ���˵�����ɣ�ֱ�ߴ�����������˶�ʱ����Բ��ƣ���

���𰸡���1��y����2��x��0.4��2+3.32����2����1m�����ܣ�![]()
��������
��1����y��a��x��0.4��2+3.32��a��0������A��0��3��������⼴�ɵó��𰸣�
��2���ٰ�y��2.6����y����2��x��0.4��2+3.32���ⷽ�����x�����ɵó�OD��1m��
�ڶ����ڵ�D��������С���ڵ�F�����ص�ʾ��ͼ��ͼ2����MD��h1��NF��h2������M��N��E���㹲��ʱ������E��EG��MD�ڵ�G����NF�ڵ�H������N��NP��MD�ڵ�P��֤����MPN�ס�NEH���ó�![]() ����NH��5MP���ֲ�ͬ�������������0��t��0.3ʱ����������0.3��t��0.65ʱ����������0.65��t��1ʱ���ֱ����t�ķ�Χ�ɵó��𰸣�
����NH��5MP���ֲ�ͬ�������������0��t��0.3ʱ����������0.3��t��0.65ʱ����������0.65��t��1ʱ���ֱ����t�ķ�Χ�ɵó��𰸣�
�⣺��1����y��a��x��0.4��2+3.32��a��0����
��x��0��y��3���룬���a����2��
�������ߵĺ�������ʽΪy����2��x��0.4��2+3.32��
��2���ٰ�y��2.6����y����2��x��0.4��2+3.32��
����ã�x��0.4��2��0.36��
���x1����0.2����ȥ����x2��1��
��OD��1m��
�ڶ�����ֱ�ߴ�����Խ��С�������ش�����E��
��ͼ1�ɵã���0��t��0.3ʱ��h2��2.2��
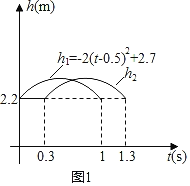
��0.3��t��1.3ʱ��h2����2��t��0.8��2+2.7��
��h1��h2��0ʱ��t��0.65��
�����ڵ�D��������С���ڵ�F�����ص�ʾ��ͼ��ͼ2��
��MD��h1��NF��h2��
����M��N��E���㹲��ʱ������E��EG��MD�ڵ�G����NF�ڵ�H������N��NP��MD�ڵ�P��
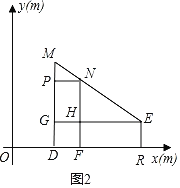
��MD��NF��PN��EG��
���M����HEN����MNP����NEH��
���MPN�ס�NEH��
��![]() ��
��
��PN��0.5��HE��2.5��
��NH��5MP��
��������0��t��0.3ʱ��
MP����2��t��0.5��2+2.7��2.2����2��t��0.5��2+0.5��
NH��2.2��1.3��0.9��
��5[��2��t��0.5��2+0.5]��0.9��
�����ã�t��0.5��2��0.16��
���![]() ����ȥ����
����ȥ����![]() ��
��
��0��t��0.3ʱ��MP��t�����������
��![]() ��
��
��������0.3��t��0.65ʱ��MP��MD��NF����2��t��0.5��2+2.7��[��2��t��0.8��2+2.7]����1.2t+0.78��
NH��NF��HF����2��t��0.8��2+2.7��1.3����2��t��0.8��2+1.4��
�ੁ2��t��0.8��2+1.4��5������1.2t+0.78����
������t2��4.6t+1.89��0��
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
��0.3��t��0.65ʱ��MP��t���������С��
��![]() ��
��
��������0.65��t��1ʱ��h1��h2�������ܣ�
�������������������������ʱ�䷶ΧΪ![]() ��
��


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45����AC = 8 cm��BC = 6 cm��EF = 9 cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB����ABC��������������DEF������ͬʱ����P����ABC�Ķ���B��������2 cm/s���ٶ���BA���A��������.����DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ��������PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ��������ʱ��Ϊt��s����0��t��4.5����
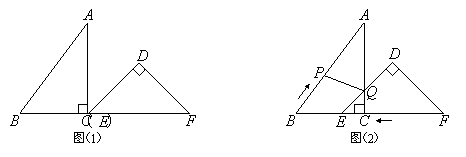
����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�鳤Ϊ40cm����Ϊ30cm�ľ���Ӳֽ����ĽǼ�ȥ�ĸ���ͬС�����Σ�Ȼ���ֽ����ı����������𣬲��ý���ճ�ã���������һ����ֽ�У�������ֽ�еĵ����Ϊ600cm2�����ȥС�����εı߳�Ϊxcm������з���Ϊ��������
A.��30��2x����40��x����600B.��30��x����40��x����600
C.��30��x����40��2x����600D.��30��2x����40��2x����600
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
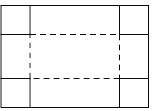
����Ŀ����һ����������̨��ͼ1��ʾ����ԭ����ͨ���ı�����֧�Ÿ˼нǵĶ�������������̨�ĸ߶ȣ�ͼ2��������������̨��ƽ��ʾ��ͼ��AB��CD��������ͬ���ȵĻ֧�Ÿˣ���O�����ǵ����ӵ㣬OA=OC��h��cm����ʾ����̨�ĸ߶ȣ�
��1����ͼ2��1����AB=CD=110cm����AOC=120������h��ֵ��
��2�������Խ��С�����֣�������������������̨�ĸ߶�Ϊ120cmʱ������֧�Ÿ˵ļнǡ�AOC��74������ͼ2��2�����������̨֧�Ÿ�AB�ij��ȣ������ȷ��lcm����
���ο����ݣ�sin37���0.6��cos37���0.8��sin53���0.8��cos53���0.6����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
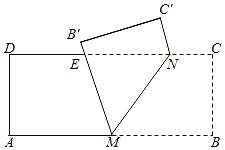
����Ŀ����ͼ����һ�ž���ֽ��ABCD��AB��5cm��BC��2cm����M��N�ֱ��ڱ�AB��CD�ϣ�CN��1cm���ֽ��ı���BCNM��MN�۵���ʹ��B��C�ֱ����ڵ�B'��C'�ϣ�����B'ǡ�����ڱ�CD��ʱ���߶�BM�ij�Ϊ_____cm���ڵ�M�ӵ�A�˶�����B�Ĺ����У�����MB'���CD���ڵ�E�����E��Ӧ�˶���·����Ϊ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
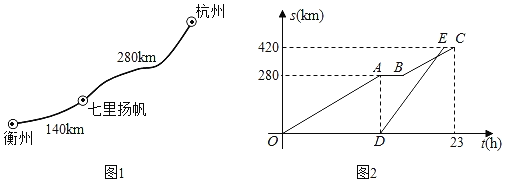
����Ŀ��2020��5��16�գ���Ǯ����ʫ·������ȫ�߿�ͨ��һ�����ִӺ��ݳ���ǰ�����ݣ���·��ͼ1��ʾ�������ֵ��ィ�¾��ڵ��������������ʱ��һ�һ�������ͬ������·�Ӻ��ݳ���ǰ�����ݣ���֪���ֵ��ٶ�Ϊ20km/h��������ʻ��ʱ���Ϊt��h���������ִ����뺼�ݵ�·��s��km������t��h����ͼ����ͼ2��ʾ��������ͣ��ǰ�����ʻ�ٶȲ��䣩��
��1��д��ͼ2��C��������ʵ�����壬��������������������ͣ����ʱ����
��2�������ֱ�������36���ӵ������ݣ��ʣ�
�ٻ��ֳ�����Сʱ�����֣�
����������ֺ�ʱ���12km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����A�ں���![]() ��ͼ���ϣ�AB��x���ڵ�B��AC��y���ڵ�C���ӳ�CA����AΪԲ��AB��Ϊ�뾶��Բ���ڵ�E���ӳ�BA����AΪԲ��AC��Ϊ�뾶��Բ���ڵ�F��ֱ��EF�ֱ�x�ᡢy���ڵ�M��N����NF��4EMʱ��ͼ����Ӱ���ֵ��������_____��
��ͼ���ϣ�AB��x���ڵ�B��AC��y���ڵ�C���ӳ�CA����AΪԲ��AB��Ϊ�뾶��Բ���ڵ�E���ӳ�BA����AΪԲ��AC��Ϊ�뾶��Բ���ڵ�F��ֱ��EF�ֱ�x�ᡢy���ڵ�M��N����NF��4EMʱ��ͼ����Ӱ���ֵ��������_____��
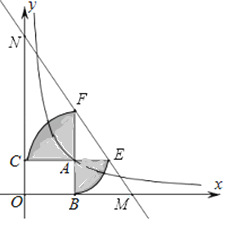
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ�����Ϸ��ĵ���O�����Ĺ�������������ڵ������γ�Բ����Ӱ����֪�����ֱ��Ϊ1.2m������������1m��������O�������3m�����������Ӱ���ֵ����Ϊ��������
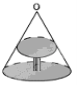
A.0.36��m2B.0.81��m2C.1.44��m2D.3.24��m2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������عˣ�
�α��о���������λ�����ʵķ���
��֪����ͼ�٣� ��֪![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �����е㣮
�����е㣮
��֤��![]() ��
��![]()
֤�����ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() �� ����
�� ����![]() ����֤��
����֤��![]() ��������
��������
�ɴ˵õ��ı���![]() Ϊƽ���ı��Σ� �����õ���֤����
Ϊƽ���ı��Σ� �����õ���֤����
��1�����������֤�����̣���������������⣺
����ͼ��������֤�����������ĸ����ߣ�����![]() Ǧ���������ߣ���
Ǧ���������ߣ���
����֤������������д���ɣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��ѡ�� .
��ѡ�� .
��������չ��
��2����ͼ�ڣ��ڵȱ�![]() �У� ��
�� ��![]() ������
������![]() ��һ���㣨��
��һ���㣨��![]() �ڵ�
�ڵ�![]() ���Ҳࣩ�����߶�
���Ҳࣩ�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ����
����![]() ���߶�
���߶�![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��
�������ж��߶�![]() ��
��![]() ��������ϵ��������֤����
��������ϵ��������֤����
����![]() �����߶�
�����߶�![]() ���ȵ���Сֵ��
���ȵ���Сֵ��
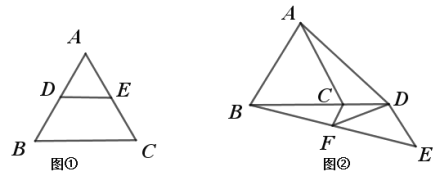
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com