某一次函数的图象经过点，且函数的值随自变量的增大而减小，请你写出一个符合上述条件的 函数解析式
y=﹣x+1（答案不唯一） ．
【考点】一次函数的性质．
【专题】开放型．
【分析】首先设一次函数解析式为 y=kx+b，根据 y 随 x 的增大而减小可选取 k=﹣1，再把点代入可 得﹣1=﹣2+b，计算出 b 的值，进而可得解析式．
【解答】解：设一次函数解析式为 y=kx+b，
∵函数的值随自变量的增大而减小，
∴k＜0，
∴可选取 k=﹣1， 再把点代入：﹣1=﹣2+b， 解得：b=1，
∴一次函数解析式为 y=﹣x+1， 故答案为：y=﹣x+1．
【点评】此题主要考查了一次函数的性质，关键是掌握一次函数 y=kx+b 中，k＜0，y 随 x 的增大而 减小，函数从左到右下降．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
已知四个三角形分别满足下列条件：①三角形的三边之比为 1：1：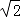
；②三角形的三边分别 是 9、40、41；③三角形三内角之比为 1：2：3；④三角形一边上的中线等于这边的一半．其中直 角三角形有（ ）个．
A．4 B．3 C．2 D．1
查看答案和解析>>
科目：初中数学 来源： 题型：
小刚想测量教学楼的高度，他用一根绳子从楼顶垂下，发现绳子垂到地面后还多了 2 米，当他把 绳子的下端拉开 6 米后，发现绳子下端刚好接触地面，则教学楼的高度是（ ）米．
A．10 B．12 C．14 D．8
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：线段 AB=20cm．
（1）如图 1，点 P 沿线段 AB 自 A 点向 B 点以 2 厘米/秒运动，点 P 出发 2 秒后，点 Q 沿线段 BA
自 B 点向 A 点以 3 厘米/秒运动，问再经过几秒后 P、Q 相距 5cm？
如图 2：AO=4cm，PO=2cm，∠POB=60°，点 P 绕着点 O 以 60 度/秒的速度逆时针旋转一周停止， 同时点 Q 沿直线 BA 自 B 点向 A 点运动，假若点 P、Q 两点能相遇，求点 Q 运动的速度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是分数
是同类项，则（﹣n）m=