
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为 . 
【答案】2或3
【解析】解:当BD=PC时,△BPD与△CQP全等,
∵点D为AB的中点,
∴BD= ![]() AB=6cm,
AB=6cm,
∵BD=PC,
∴BP=8﹣6=2(cm),
∵点P在线段BC上以2厘米/秒的速度由B点向C点运动,
∴运动时间时1s,
∵△DBP≌△PCQ,
∴BP=CQ=2cm,
∴v=2÷1=2;
当BD=CQ时,△BDP≌△QCP,
∵BD=6cm,PB=PC,
∴QC=6cm,
∵BC=8cm,
∴BP=4cm,
∴运动时间为4÷2=2(s),
∴v=6÷2=3(m/s),
故答案为:2或3.
此题要分两种情况:①当BD=PC时,△BPD与△CQP全等,计算出BP的长,进而可得运动时间,然后再求v;②当BD=CQ时,△BDP≌△QCP,计算出BP的长,进而可得运动时间,然后再求v.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
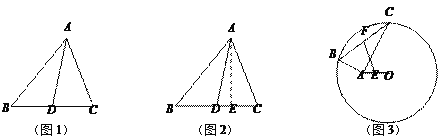
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.
小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=……
(1)请你完成小明剩余的证明过程;
理解运用:
(2) ① 在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=_______;
② 如图3,⊙O的半径为6,点A在圆内,且OA=2![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
拓展延伸:
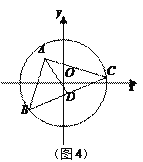
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5![]() ,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是 分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1). 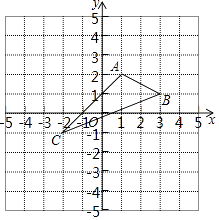
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1 .
(2)写出点A1 , B1 , C1的坐标(直接写答案)
A1
B1
C1
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
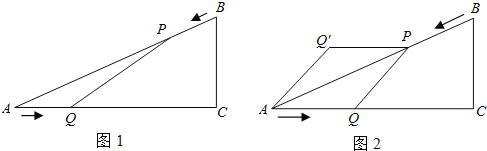
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6 cm ,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm /s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.
(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com