
【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

【答案】(1)证明见解析;
(2)FG的长为![]() .
.
【解析】试题分析:(1)连接OD,证∠ODF=90°即可.
(2)利用△ADF是30°的直角三角形可求得AF长,同理可利用△FHC中的60°的三角函数值可求得FG长.
试题解析:(1)连接OD,

∵以等边三角形ABC的边AB为直径的半圆与BC边交于点D,
∴∠B=∠C=∠ODB=60°,
∴OD∥AC,
∵DF⊥AC,
∴∠CFD=∠ODF=90°,即OD⊥DF,
∵OD是以边AB为直径的半圆的半径,
∴DF是圆O的切线;
(2)∵OB=OD=![]() AB=6,且∠B=60°,
AB=6,且∠B=60°,
∴BD=OB=OD=6,
∴CD=BC﹣BD=AB﹣BD=12﹣6=6,
∵在Rt△CFD中,∠C=60°,
∴∠CDF=30°,
∴CF=![]() CD=
CD=![]() ×6=3,
×6=3,
∴AF=AC﹣CF=12﹣3=9,
∵FG⊥AB,
∴∠FGA=90°,
∵∠FAG=60°,
∴FG=AFsin60°=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
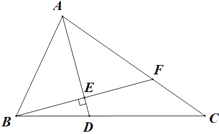
【题目】如图,在△ABC中,∠ABC=65°,∠C=35°,AD是△ABC的角平分线.
(1)求∠ADC的度数.
(2)过点B作BE⊥AD于点E,BE延长线交AC于点F.求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠ACB是直角,∠ABC=60°,AD、CE、BF分别是∠BAC、∠BCA、∠ABC的平分线,AD、CE、BF相交于点F.
①请求出∠AFC的度数并说明理由;
②请你判断FE与FD之间的数量关系并说明理由。
(2)如图2,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请判断线段AE、CD、AC之间的数量关系并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形平移与旋转”为主题开展数学活动,![]() 和
和![]() 是两个等边三角形纸片,其中,
是两个等边三角形纸片,其中,![]() .
.
解决问题
(1)勤奋小组将![]() 和
和![]() 按图1所示的方式摆放(点
按图1所示的方式摆放(点![]() 在同一条直线上) ,连接
在同一条直线上) ,连接![]() .发现
.发现![]() ,请你给予证明;
,请你给予证明;

(2)如图2,创新小组在勤奋小组的基础上继续探究,将![]() 绕着点
绕着点![]() 逆时针方向旋转,当点
逆时针方向旋转,当点![]() 恰好落在
恰好落在![]() 边上时,求
边上时,求![]() 的面积;
的面积;

拓展延伸
(3)如图3,缜密小组在创新小组的基础上,提出一个问题: “将![]() 沿
沿![]() 方向平移
方向平移![]() 得到
得到![]() 连接
连接![]() ,当
,当![]() 恰好是以
恰好是以![]() 为斜边的直角三角形时,求
为斜边的直角三角形时,求![]() 的值.请你直接写出
的值.请你直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数![]() 的图象与性质.
的图象与性质.
因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
| … |
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 |
|
| 1 |
|
| … |
| … |
|
| 2 | 3 | 5 |
|
| 0 |
|
| … |
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出了相应的点(如图所示).
相应的函数值为纵坐标,描出了相应的点(如图所示).
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而 ;(填“增大”或“减小”)
的增大而 ;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③![]() 图象关于点 成中心对称.(填点的坐标)
图象关于点 成中心对称.(填点的坐标)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=2x+2与直线 l2:y2=mx+8相交于点 P(2,b).
(1)求 b,m 的值;
(2)直接写出当 y1<y2 时,自变量 x 的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式,例如:![]() ,
,![]() ,
,![]() ,…含有两个字母
,…含有两个字母![]() ,
,![]() 的对称式的基本对称式是
的对称式的基本对称式是![]() 和
和![]() ,像
,像![]() ,
,![]() 等对称式都可以用
等对称式都可以用![]() ,
,![]() 表示,例如:
表示,例如:![]() .
.
请根据以上材料解决下列问题:
(1)式子:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,属于对称式的是 (填序号)
中,属于对称式的是 (填序号)
(2)已知![]() .
.
①若![]() ,求对称式
,求对称式![]() 的值
的值
②若![]() ,求对称式
,求对称式![]() 的最大值
的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com