

分析 (1)如图1中,连接OF、OB,设OA交BF于H.只要证明△AOF是等边三角形即可解决问题;
(2)如图2中,连接AC、AE、EC、BC、CD、PC,在PC上截取PH=PA,连接AH,作CN⊥PD于N,CM⊥PB于M.只要证明PA+PE=PC,PB+PD=$\sqrt{3}$PC,即可解决问题;
(3)利用(2)中结论,求出PC的最大值以及最小值即可解决问题;
解答 解:(1)如图1中,连接OF、OB,设OA交BF于H.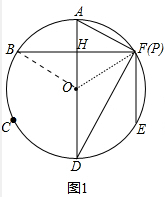
由题意∠AOB=∠AOF=60°,$\widehat{AB}$=$\widehat{AF}$,
∴OA⊥BF,BH=FH,
∵OA=OF,
∴△AOF是等边三角形,
∴PA=OA=6,FH=OF•sin60°=3$\sqrt{3}$,
∴PB=2HF=6$\sqrt{3}$,
∴PA+PB=6+3$\sqrt{3}$.
(2)如图2中,连接AC、AE、EC、BC、CD、PC,在PC上截取PH=PA,连接AH,作CN⊥PD于N,CM⊥PB于M.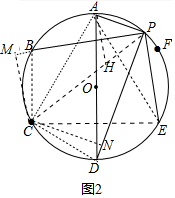
易知△ACE是等边三角形,
∴∠APC=∠AEC=60°,
∵PA=PH,
∴△APH是等边三角形,
∴PA=AH=PH,AC=AE,∠CAE=∠HAP,
∴∠CAH=∠EAP,
∴△ACH≌△AEP,
∴PE=CH,
∴PA+PE=PH+CH=PC,
∵∠CPB=∠CPD=30°,CN⊥PD于N,CM⊥PB于M,
∴CN=CM,
∵$\widehat{BC}$=$\widehat{CD}$,
∴CB=CD,
∴Rt△PCM≌Rt△PCN,Rt△CMB≌Rt△CND,
∴PM=PN,BM=DN,
∴PB+PD=(PM-BM)+(PN+DN)=2PN=2PC•cos30°=$\sqrt{3}$PC,
∴$\frac{PA+PE}{PB+PD}$=$\frac{PC}{\sqrt{3}PC}$=$\frac{\sqrt{3}}{3}$.
(3)由(2)可知PA+PE=PC,PB+PD=$\sqrt{3}$PC,
∴t=PA+PB+PD+PE=(1+$\sqrt{3}$)PC,
∵6$\sqrt{3}$≤PC≤12,
∴6$\sqrt{3}$+18≤t≤12+12$\sqrt{3}$.
点评 本题考查圆综合题、圆周角定理、等边三角形的判定和性质.角平分线的性质定理、全等三角形的判定和性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
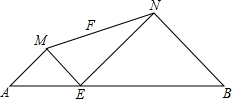 如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.
如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知三点A、B、C.
如图,已知三点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
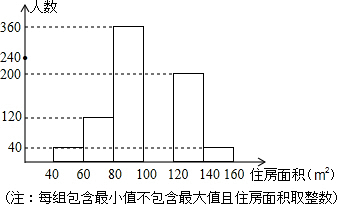 某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:
某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:| 年收入(万元) | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| 被调查的消费者数(人) | 200 | 300 | 400 | 70 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=0 | B. | x=1 | C. | x=-1 | D. | x=$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
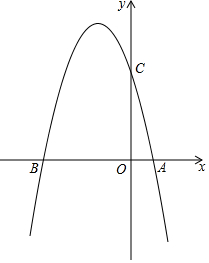 如图,已知抛物线经过A(1,0),C(0,4)两点,交x轴于另一点B,其对称轴是x=-1.5.
如图,已知抛物线经过A(1,0),C(0,4)两点,交x轴于另一点B,其对称轴是x=-1.5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com