
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
①当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
②当点![]() 落在第二象限内,
落在第二象限内,![]() 取得最小值时,求
取得最小值时,求![]() 的值.
的值.
【答案】(1)![]() ,顶点的坐标为(1,-4);(2)
,顶点的坐标为(1,-4);(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1) 抛物线![]() 经过点
经过点![]() ,代入求得b值即可求得抛物线的解析式,把抛物线化为顶点式,直接写出顶点坐标即可;(2)①由点P(m,t)在抛物线
,代入求得b值即可求得抛物线的解析式,把抛物线化为顶点式,直接写出顶点坐标即可;(2)①由点P(m,t)在抛物线![]() 上,可得
上,可得![]() ,
,
![]() 关于原点的对称点为
关于原点的对称点为![]() ,可得P’(-m,-t),即可得
,可得P’(-m,-t),即可得![]() ,所以
,所以![]() ,解方程即可求得m的值;②构造
,解方程即可求得m的值;②构造![]() 与t的二次函数模型,根据二次函数的性质求得
与t的二次函数模型,根据二次函数的性质求得![]() 的值最小是t的值,再代入二次函数
的值最小是t的值,再代入二次函数![]() 中求得m的值即可.
中求得m的值即可.
试题解析:(1)∵抛物线![]() 经过点
经过点![]() ,
,
∴0=1-b-3,解得b=-2.
∴抛物线的解析式为![]() ,
,
∵![]() ,
,
∴顶点的坐标为(1,-4).
(2)①由点P(m,t)在抛物线![]() 上,有
上,有![]() .
.
∵![]() 关于原点的对称点为
关于原点的对称点为![]() ,有P’(-m,-t).
,有P’(-m,-t).
∴![]() ,即
,即![]()
∴![]()
解得![]()
②由题意知,P’(-m,-t)在第二象限,
∴-m<0,-t>0,即m>0,t<0.
又抛物线![]() 的顶点的坐标为(1,-4),得-4≤t<0.
的顶点的坐标为(1,-4),得-4≤t<0.
过点P’作P’H⊥x轴,H为垂足,有H(-m,0).
又![]() ,
,![]() ,
,
则![]()
当点A和H不重合时,在Rt△P’AH中,![]()
当点A和H重合时,AH=0, ![]() ,符合上式.
,符合上式.
∴![]() ,即
,即![]()
记![]() ,则
,则![]() ,
,
∴当t=-![]() 时,y’取得最小值.
时,y’取得最小值.
把t=-![]() 代入
代入![]() ,得
,得![]()
解得![]()
由m>0,可知![]() 不符合题意
不符合题意
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】小李和小陆从 A 地出发,骑自行车沿同一条路行驶到 B 地,他们离出发地的距离s和行驶时间t之间的关系的图象如图,根据图象回答下列问题: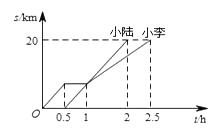
(1)小李在途中逗留的时间为h,小陆从 A 地到 B 地的速度是km/h.
(2)当小李和小陆相遇时,他们离 B 地的路程是千米;
(3)写出小李在逗留之前离 A 地的路程s和行驶时间t之间的函数关系式为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com