
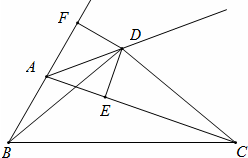
如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF ;②CE=AB+AE;③∠DBF=∠DCE;④∠DAE=∠DAF.其中正确的结论有( )
;②CE=AB+AE;③∠DBF=∠DCE;④∠DAE=∠DAF.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
科目:初中数学 来源: 题型:
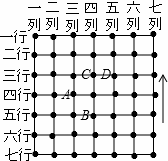
如图所示,有一个方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么B的位置是( )
A.(4,5) B.(5,4) C.(4,2) D.(4,3)
B.
查看答案和解析>>
科目:初中数学 来源: 题型:
对一张矩形纸片 ABCD进行折叠,具体操作如下:
ABCD进行折叠,具体操作如下:
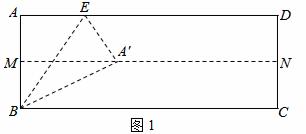
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点 处,并使折痕经过点B,得到折痕BE,同时,得到线段
处,并使折痕经过点B,得到折痕BE,同时,得到线段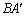 ,
,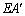 ,展开,如图1;
,展开,如图1;
第三步:再沿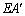 所在的直线折叠,点B落在AD上的点
所在的直线折叠,点B落在AD上的点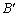 处,
处, 得到折痕EF,同时得到线段
得到折痕EF,同时得到线段 ,展开,如图2
,展开,如图2 .
.
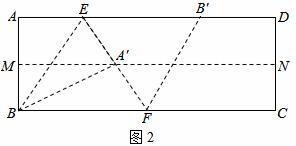
求∠ABE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图, 在△ABC中,AB=AC,∠BAC=30°.点D为△ABC内一点,且DB=DC,∠DCB=30°.点E为BD
在△ABC中,AB=AC,∠BAC=30°.点D为△ABC内一点,且DB=DC,∠DCB=30°.点E为BD 延长线上一
延长线上一 点,且A
点,且A E=AB.
E=AB.
(1)求∠ADE的度数;
(2)若点M在DE上,且DM=D
 A,求证:ME=DC.
A,求证:ME=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图9,已知二次函数y=ax2+bx+2的图像经过A(-1,-1),C(1,3).
(1)求二次函数的解析式并画出它的图像;
(2)直接写出点A关于抛物线对称轴的对称点A'的坐标;
(3)求该抛物线上到x轴的距离为2的所有点的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中
①方程x(x-2)=x-2的解是x=1;
②小明沿着坡度为1:2的山坡向上走了1000m,则他升高了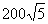 m;
m;
③若直角三角形的两边长为3和4,则第三边的长为 5
④将抛物线 向左平移2个单位后,得到的抛物线的解析式是
向左平移2个单位后,得到的抛物线的解析式是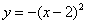 .
.
正确的命题有( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com