
分析 (1)设租用甲种货车x辆,乙种货车为(8-x)辆,根据题意列出一元一次不等式组,解不等式组求出x的范围,即可得出结果;
(2)设总费用为y元,租用甲种货车x辆,乙种货车为(8-x)辆,根据题意得出y是x的一次函数,即可得出结论.
解答 解:(1)设租用甲种货车x辆,乙种货车为(8-x)辆,
根据题意得:$\left\{\begin{array}{l}{20x+8(8-x)≥100}\\{6x+8(8-x)≥54}\end{array}\right.$,
解得:3≤x≤5.
所以甲可取3,4,5,因此有3种方案.分别为:
①租用甲3辆时,乙为5辆,
②租用甲4辆时,乙为4辆,
③租用甲5辆时,乙为3辆;
(2)设总费用为y元,租用甲种货车x辆,乙种货车为(8-x)辆,
∵y=2 000x+2 500(8-x)=-500x+20 000,
∴y=-500x+20 000,
∵-500<0,
∴y随x的增大而减小,
∴当x取最大值5时,y有最小值17 500元.
答:当租用甲5辆时,乙为3辆时,运费最少;最少运费是17 500元.
点评 本题考查了一元一次不等式组的应用、一次函数的应用;根据题意中的数量关系列出不等式组或得出函数关系式是解决问题的关键.


科目:初中数学 来源: 题型:填空题
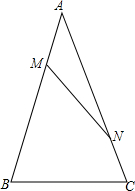 如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.
如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
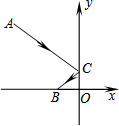 如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )
如图,一束光线从点A(-3,3)出发,经过y轴上的点C反射后经过点B(-1,0),则光线从点A到点B经过的路线长是( )| A. | 3 | B. | $\frac{7}{2}$ | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3).将矩形PMON绕点0顺时针旋转90°得到矩形P′M′O′M′
如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3).将矩形PMON绕点0顺时针旋转90°得到矩形P′M′O′M′查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com