
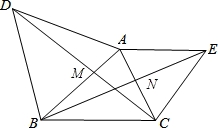
如图,△ABD、△AEC都是等边三角形.AB、CD相交于M,AC、BE相交于N,∠MAN=60°.求证:
(1)BE=DC;
(2)AM=AN.
【考点】全等三角形的判定与性质;等边三角形的性质.
【专题】证明题.
【分析】(1)由等边三角形的性质得出AB=AD,AE=AC,∠BAD=∠CAE=60°,证出 ∠BAE=∠DAC,根据SAS证明△ABE≌△ADC,得出对应边相等即可;
∠BAE=∠DAC,根据SAS证明△ABE≌△ADC,得出对应边相等即可;
(2)证△ADM≌△ABN即可;
【解答】证明:(1)∵△ABD、△AEC都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAE=∠DAC,
在△ABE和△ADC中,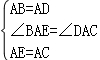 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC;
(2)∵△ABE≌△ADC,
∴∠ADM=∠ABN,
在△ADM与△ABN中,
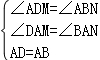 ,
,
∴△ADM≌△ABN(AAS),
∴AM=AN.
【点评】此题主要考查了全等三角形的判定和性质定理、等边三角形的性质,关键是找出或证明能使三角形全等的条件.对于全等三角形的判定定理SAS,ASA,AAS,SSS,HL必须熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
已知:如图,菱形ABCD的四边相等,且对角线互相垂直平分.在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有( )
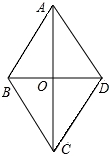
A.7对 B.8对 C.9对 D.10对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com