
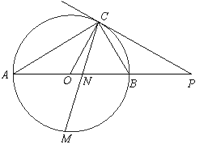
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
【答案】(1)证明见解析;(2)8.
【解析】试题分析:(1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是 O的切线;(2)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MNMC;代入数据可得MNMC=BM2=8.
试题解析:(1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°,OC⊥CP.
∵OC是O的半径,
∴PC是O的切线。
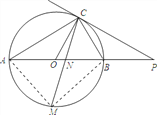
(2)连接MA,MB,
∵点M是![]() 的中点,
的中点,
∴![]() =
=![]() .
.
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴![]() .
.
∴BM2=MNMC.
又∵AB是O的直径,AM=BM,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=![]() .
.
∴MNMC=BM2=8.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】办公中常用到的纸张一般是A4纸,其厚度约为0.0075m,用科学记数法表示为( )
A. 7.5×10﹣3m B. 7.5×10﹣2m C. 7.5×103m D. 75×10﹣3m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·大庆中考)如图,P1、P2是反比例函数y=![]() (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(1)求反比例函数的解析式;
(2)①求P2的坐标;②根据图象直接写出在第一象限内当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y=![]() 的函数值.
的函数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:
得分(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 7 | 12 | 10 | 8 | 3 |
则得分的众数和中位数分别为( )
A.70分,70分
B.80分,80分
C.70分,80分
D.80分,70分
查看答案和解析>>
科目:初中数学 来源: 题型:
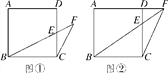
【题目】已知正方形ABCD,点E在边CD上,点F在线段BE的延长线上,连接FC,且∠FCE=∠CBE.
(1)如图①,当点E为CD边的中点时,求证:CF=2EF;
(2)如图②,当点F位于线段AD的延长线上时,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com