
����Ŀ����ÿ��С�����εı߳�Ϊ1�������У�ÿ��С�����εĶ����Ϊ��㣮���ǽ���һ������ƶ�����֮���![]() ����һ�������˶���Ϊһ�������任��
����һ�������˶���Ϊһ�������任��
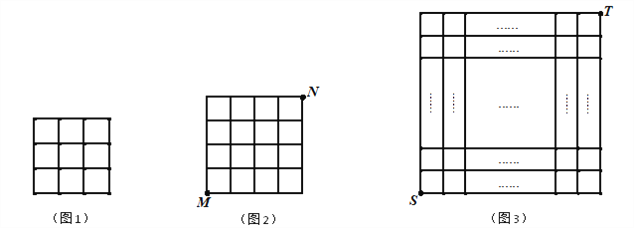
��1����ͼ1�л����߳�Ϊ![]() �������Σ�ʹ���Ķ���������ĸ���ϣ�
�������Σ�ʹ���Ķ���������ĸ���ϣ�
��2����ͼ2����һֻ����С���Ӹ��![]() ���������������任����������Եĸ��
���������������任����������Եĸ��![]() ����������Ҫ�����任�Ĵ����� �Σ�
����������Ҫ�����任�Ĵ����� �Σ�
��3����ͼ3����![]() �������������У�һֻ����С���Ӹ��
�������������У�һֻ����С���Ӹ��![]() �������ɴ������任����������Եĸ��
�������ɴ������任����������Եĸ��![]() ���������������·��Ϊ ��
���������������·��Ϊ ��
���𰸡���1����ͼ����������2��4����3��14![]()
�������������������1��.�������⻭��ͼ�μ��ɣ���2��.�������⻭��ͼ�ν�𣻣�3�����ݴ�һ������ƶ�����֮���![]() ����һ�������˶���Ϊһ�������任,�������A-C-F�ķ��������任10�κ��S��λ��,�ٸ��ݵ�T��λ�ý����ʵ��ı任,���ɵõ��任�ܴ���.
����һ�������˶���Ϊһ�������任,�������A-C-F�ķ��������任10�κ��S��λ��,�ٸ��ݵ�T��λ�ý����ʵ��ı任,���ɵõ��任�ܴ���.
�⣺��1����ͼ1��
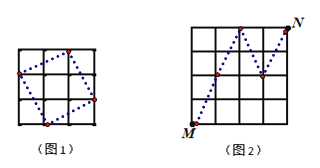
��2����ͼ2��������Ҫ�����任�Ĵ�����4��.
��3����ͼ3, ![]() ,
,
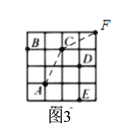
![]() ���α任�൱�������ƶ�3��,�����ƶ�3��,
���α任�൱�������ƶ�3��,�����ƶ�3��,
����![]() ,
,
![]() (��������)��
(��������)��
![]() ��A-C-F�ķ��������任10�κ�,�൱�������ƶ���10��2��3=15��,�����ƶ���10��2��3=15��,��ʱSλ����ͼ��ʾ��5��5������������ĵ�G��,�ٰ���ͼ��ʾ�ķ�ʽ�任4�μ��ɵ����T��,
��A-C-F�ķ��������任10�κ�,�൱�������ƶ���10��2��3=15��,�����ƶ���10��2��3=15��,��ʱSλ����ͼ��ʾ��5��5������������ĵ�G��,�ٰ���ͼ��ʾ�ķ�ʽ�任4�μ��ɵ����T��,
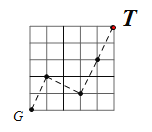
![]() �Ӹ������εĶ���S���������任����������ԵĶ���T,������Ҫ�����任�Ĵ�����14��,
�Ӹ������εĶ���S���������任����������ԵĶ���T,������Ҫ�����任�Ĵ�����14��,
�������������·��Ϊ![]() .
.


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD�Ǹߣ�AE��BF�ǽ�ƽ���ߣ������ཻ�ڵ�O����CAB=500����C=600������DAE����BOA�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
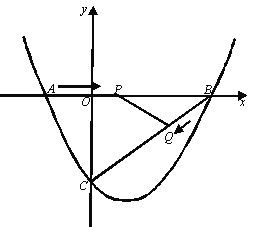
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��x�ύ�ڵ�A(
��x�ύ�ڵ�A(![]() ��0)��B(4��0)���㣬��y�ύ�ڵ�C��
��0)��B(4��0)���㣬��y�ύ�ڵ�C��
������1���������ߵĽ���ʽ��
������2����P��A����������߶�AB����ÿ��3����λ���ȵ��ٶ���B���˶���ͬʱ��Q��B����������߶�BC����ÿ��1����λ������C���˶�������һ���㵽���յ�ʱ����һ����Ҳֹͣ�˶�������PBQ����ʱ�����˶�������ʹ��PBQ���������������Ƕ��٣�
��3������PBQ��������ʱ����BC�·����������ϴ��ڵ�K��ʹS��CBK��S��PBO=5��2����K�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣�ʵʩ�¿γ̸ĸ��ѧ��������ѧϰ���������������кܴ���ߣ�����ʦΪ���˽����̰༶ѧ������ѧϰ�����������ľ���������Ա��ಿ��ѧ��������Ϊ�������µĸ��ٵ��飬�����������ֳ����࣬A���ر�ã�B���ã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺

��1�����ε����У�����ʦһ�������� ��ͬѧ������C��Ů���� ����D�������� ����
��2�������������ͳ��ͼ����������
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���зֱ�ѡȡһλͬѧ���С�һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
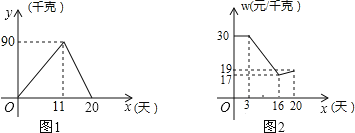
����Ŀ��С���ҽ�����ֲ�IJ�ݮϲ����գ���ժ����20��ȫ�������꣬�ְ������Խ��������������и��ټ�¼��С��������ѧ����ѧ֪ʶ����¼������ͼ������ͼ���Ϊ�߶Σ�����������y����λ��ǧ�ˣ�������ʱ��x����λ���죩�ĺ�����ϵ��ͼ1��ʾ����ݮ�ļ۸�w����λ��Ԫ/ǧ�ˣ�������ʱ��x����λ���죩�ĺ�����ϵ��ͼ2��ʾ��
��1���۲�ͼ��ֱ��д����0��x��11ʱ����������y������ʱ��x֮��ĺ�������ʽΪ ��
��11��x��20ʱ����������y������ʱ��x֮��ĺ�������ʽΪ ��
��2���������11������۽�
��3�������е�15��ʱ���ְְѵ��������۵IJ�ݮ���������ھ������壬������Ϊÿǧ��15Ԫ�������嵽�г����յ��յļ۸�wԪ/ǧ�˽��������IJ�ݮȫ�������꣬�������۵Ĺ����У���ݮ�����������2%����ô��������֧�������س���20Ԫ������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¸������ʽ����ĸa�������е��ǣ� ��
A.3a+a2+2
B.a2+2+3a
C.2+3a+a2
D.a2+3a+2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����������ţ�������������ˮλABʱ��20�ף�ˮλ����3�ʹﵽ������CD����ʱˮ�����Ϊ10�ף�����ˮ����ʱ��ˮλ��ÿСʱ0.2���ٶ������Ӿ����߿�ʼ���ٳ�������Сʱ���ܵ����Ŷ�����ƽ��ֱ������ϵ�����Ŷ���Ϊ��O�ģ� 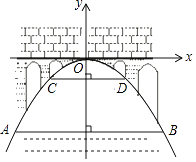
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com