
【题目】某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
(1)甲车间每小时生产产品 件,a= .
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?

【答案】(1)60,![]() 小时;
小时;
(2)乙车间更换新设备之后y与x之间的函数关系式为:y=160x﹣190,
∴m=450件;
(3)两个车间完成原任务量需要的时间是![]() 小时.
小时.
【解析】
试题分析:(1)由开始甲、乙两个车间工作效率相同,于是得到开始甲、乙两个车间工作效率是每小时生产产品60个,即可得到结论;
(2)设乙车间更换新设备之后y与x之间的函数关系式为:y=kx+b,把(![]() ,210),(3,290)代入y=kx+b列方程组即可得到结论;
,210),(3,290)代入y=kx+b列方程组即可得到结论;
(3)根据两个车间完成原任务量需要的时间=乙车间更换新设备前的时间+乙车间更换新设备中的时间+乙车间更换新设备后的时间,即可得到结论.
试题解析:(1)∵开始甲、乙两个车间工作效率相同,
∴开始甲、乙两个车间工作效率是每小时生产产品60个,
∴a=![]() +1=
+1=![]() 小时,
小时,
故答案为:60,![]() 小时;
小时;
(2)设乙车间更换新设备之后y与x之间的函数关系式为:y=kx+b,
把(![]() ,210),(3,290)代入y=kx+b得:
,210),(3,290)代入y=kx+b得: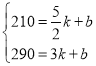 ,
,
∴![]() ,
,
∴乙车间更换新设备之后y与x之间的函数关系式为:y=160x﹣190,
当x=4时,y=450,
∴m=450件;
(3)两个车间完成原任务量需要的时间=乙车间更换新设备前的时间+乙车间更换新设备中的时间+乙车间更换新设备后的时间,
即1+(![]() ﹣1﹣
﹣1﹣![]() )﹣
)﹣
答:两个车间完成原任务量需要的时间是![]() 小时.
小时.



 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2是
A. 含30°角的直角三角形 B. 顶角是30的等腰三角形
C. 等边三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( ) 
A.16cm2
B.20cm2
C.80cm2
D.160cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A.4 B.6 C.8 D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com