
分析 根据“正方体的每一条棱长是一个一位数,表面积的每个正方形面积是一个两位数,整个表面积是一个三位数”的条件,可以判断正方体的棱长有5,6,7,8,9这五种可能性.然后分别计算出每个正方体一个面的面积和正方体的表面积,然后进行推理判断.
解答 解:根据“正方体的每一条棱长是一个一位数,表面积的每个正方形面积是一个两位数,整个表面积是一个三位数”的条件,可以判断正方体的棱长有5,6,7,8,9这五种可能性.
填表如下:
| 棱长 | 5 | 6 | 7 | 8 | 9 |
| 正方形面积 | 25 | 36 | 49 | 64 | 81 |
| 全面积 | 150 | 216 | 294 | 384 | 486 |
点评 此题主要考查正方体的表面积和体积的计算,能够根据正方体的表面积和体积的计算方法解决有关的实际问题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
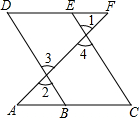 推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
推理填空:如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
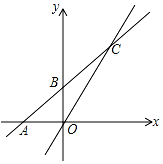 已知一次函数y=kx+b 的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
已知一次函数y=kx+b 的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com