
 如图,已知菱形ABCD的边长是13,O是对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.若菱形一条对角线长为10,则图中阴影部分的面积为60.
如图,已知菱形ABCD的边长是13,O是对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.若菱形一条对角线长为10,则图中阴影部分的面积为60.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
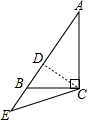 如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,点D是AB边上的一点,沿CD折叠△ABC,若点A落在AB的延长线上的点E处,则AD的长为6.4.
如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,点D是AB边上的一点,沿CD折叠△ABC,若点A落在AB的延长线上的点E处,则AD的长为6.4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -2 | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
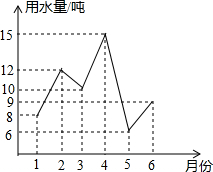 为了了解家里的用水情况,以便能更好的节约用水,小方把自己家1至6月份的用水量绘制成如图的折线图,那么小方家这6个月的月用水量最大是( )
为了了解家里的用水情况,以便能更好的节约用水,小方把自己家1至6月份的用水量绘制成如图的折线图,那么小方家这6个月的月用水量最大是( )| A. | 1月 | B. | 4月 | C. | 5月 | D. | 6月 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com