
【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2). 表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表2中,a= , b=;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E是边BC上的两个点,且BD=DE=EC,过点C作CF∥AB交AE延长线于点F,连接FD并延长与AB交于点G; 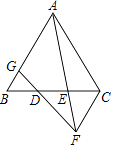
(1)求证:AC=2CF;
(2)连接AD,如果∠ADG=∠B,求证:CD2=ACCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:如图,已知抛物线y=﹣x2+2x+3的图象与x轴交于点A,B(A在B的右侧),与y轴交于点C,对称轴与抛物线交于点D,与x轴交于点E.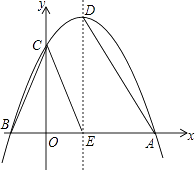
(1)求点A,B,C,D的坐标;
(2)求出△ACD的外心坐标;
(3)将△BCE沿x轴的正方向每秒向右平移1个单位,当点E移动到点A时停止运动,若△BCE与△ADE重合部分的面积为S,运动时间为t(s),请直接写出S关于t的函数关系式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=4,AC=2,BC=2 ![]() ,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E. 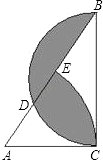
(1)以BC为直径的圆与AC所在的直线有何位置关系?请说明理由;
(2)求图中阴影部分的面积(结果可保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D. 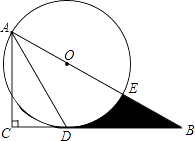
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°. ①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( ) 
A.10m
B.12m
C.12.4m
D.12.32m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com