
����Ŀ���ۺ���̽������ͼ����֪������y=��x2+2x+3��ͼ����x�ύ�ڵ�A��B��A��B���Ҳࣩ����y�ύ�ڵ�C���Գ����������߽��ڵ�D����x�ύ�ڵ�E��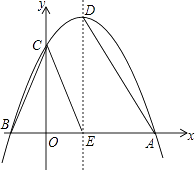
��1�����A��B��C��D�����ꣻ
��2�������ACD���������ꣻ
��3������BCE��x���������ÿ������ƽ��1����λ������E�ƶ�����Aʱֹͣ�˶�������BCE���ADE�غϲ��ֵ����ΪS���˶�ʱ��Ϊt��s������ֱ��д��S����t�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
���𰸡�
��1��
�⣺��y=0ʱ����x2+2x+3=0����ã�x1=��1��x2=3
���A������3��0������B��������1��0����
��x=0ʱ�����멁x2+2x+3=0��y=3��
��C��������0��3��
��y=��x2+2x+3=����x��1��2+4��
��D���������1��4��
��2��
�⣺����D��DF��y�ᣬ����ΪF������AC��CD����ͼ1
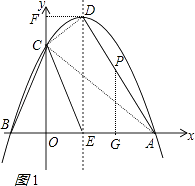
��A��3��0����C��0��3����D��1��4��
��DF=CF=1��OC=AC=3��
���DFC����AOC��Ϊ����ֱ�������Σ�
���DCF=��ACO=45�㣬���ACD=90�㣬��ACDΪֱ�������Σ�
��б��AD���е�Ϊ��ACD�����ģ����PΪAD���е㣬
����P��PG��OA������ΪG��
�ߡ�APG�ס�ADE��
���GΪEA���е㣬
��OG=2��PG=2��
���P������2��2��
��3��
�⣺��ͼ2����0��t��1ʱ��EE��=t
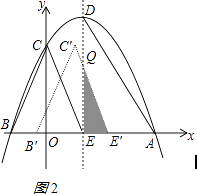
��E��C����DE���ڵ�Q�����ݡ�QEE�䡫��COB�����QE=3t��
��S= ![]() QEEE��=
QEEE��= ![]() ��t��3t=
��t��3t= ![]() t2��
t2��
��ͼ3����1��t�� ![]() ʱ���赱B��C����DE���ڵ�H��
ʱ���赱B��C����DE���ڵ�H��
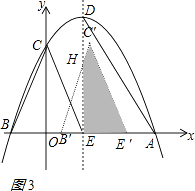
���ݡ�B��HE����BOC�����EH=3��2��t����
��S=S��C��B��E����S��HB��E��
��S= ![]() ��2��3��
��2��3�� ![]() ��3��2��t��2
��3��2��t��2
��S=�� ![]() t2+6t��3��
t2+6t��3��
��ͼ4���� ![]() ��t��2ʱ��
��t��2ʱ��
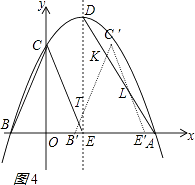
��ֱ��B��C����ֱ��DE����ΪT����ֱ��AD�Ľ���ΪK��ֱ��AD��ֱ��E��C��Ľ���ΪL��
��B�䣨t��1��0����C�䣨t��3����E�䣨t+1��0����
��ֱ��B��C��Ľ���ʽΪ��y=3x+��3��3t����
ֱ��E��C��Ľ���ʽΪ��y=��3x+��3+3t����
��ֱ��AD�Ľ���ʽΪy=2x+6��
�߽ⷽ���� ![]()
��� 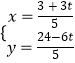
��K�� ![]() ��
�� ![]() ��
��
�ⷽ���� ![]()
��� ![]()
��L��3t��3����6t+12����
�֡�T��1��6��3t����
��DT=4����6��3t��=3t��2��AE��=3����t+1��=2��t����DKT��DTΪ�ױ��ϵĸ�Ϊ�� ![]() ��1=
��1= ![]() ��
��
S=S��EAD��S��DKT��S��E��AL=4�� ![]() ��3t��2��
��3t��2�� ![]() ��
�� ![]() ��2��t������6t+12����
��2��t������6t+12����
��S=�� ![]() t2+
t2+ ![]() ��
�� ![]() ��
��
�൱0��t��1ʱ��S= ![]() t2
t2
��1��t�� ![]() ʱ��S=��
ʱ��S=�� ![]() t2+6t��3
t2+6t��3
�� ![]() ��t��2ʱ��S=��
��t��2ʱ��S=�� ![]() t2+
t2+ ![]() ��
�� ![]()
����������1�����ú�����ϵʽ�ֱ���x=0��y=0�������A��B����C���꣬ͨ���䷽����õ�D���ꣻ��2����DF��y�ᣬ����DC��AC�����������֤����ACDΪֱ�������Σ���ͨ�����������ζ�Ӧ�ߵıȿɵó����ĵ����ꣻ��3�������˶�ʱ��t���ֳ�0��t��1��1��t�� ![]() ��
�� ![]() ��t��2��������������ۣ�����ֱ�߽���ʽ����������꣬�Ӷ�������ֱ��ʾ������
��t��2��������������ۣ�����ֱ�߽���ʽ����������꣬�Ӷ�������ֱ��ʾ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� 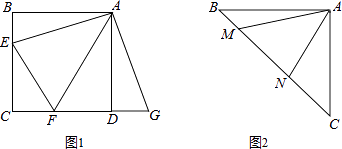
��1����ͼ1��������ABCD�У���E��F�ֱ��ڱ�BC��CD�ϣ���EAF=45�㣬�ӳ�CD����G��ʹDG=BE������EF��AG����֤��EF=FG��
��2����ͼ������ֱ��������ABC�У���BAC=90�㣬AB=AC����M��N�ڱ�BC�ϣ��ҡ�MAN=45�㣬��BM=1��CN=3����MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M�ǡ�ABC�Ľ�ƽ����AT���е㣬��D��E�ֱ���AB��AC���ϣ��߶�DE����M���ҡ�ADE=��C����ô��ADE�͡�ABC��������� �� 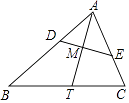
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У��Գ���ƽ����y��������߹���A��1��0����B��3��0����C��4��6����
��1���������ߵı���ʽ��
��2���ֽ�������������x�᷽������ƽ��6����λ������y�᷽��ƽ��k����λ����������������x�ύ�ڵ�D��E����D�ڵ�E����ߣ�����ʹ��ACD�ס�AEC������A��C��D���ζ�Ӧ����A��E��C��������k��ֵ����ע������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼ӿ���ʡ���繫·���裬��ʡ�ƻ���ʮ���塱�ڼ���ٹ�·��Ӫ��̴�1000�����һ����������������ͨ����ij�ؼƻ���һ�����ٹ�·������Сɽ��������A��B֮�俪ͨһ�����������̼�����Ա�����������Сɽ����A��B֮��ľ�������˲��������Ǵ�A����������������������������Ӱ�죬��������30��/�ֵ��ٶ���������75��ǵķ�����У�25���Ӻ�C������ʱ�������ϵ��˲��Сɽ����B��ĸ���Ϊ30�㣬��Сɽ��������A��B�����ľ���Ϊ�����ף�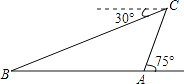
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��ѡ��ѧ���μӡ�������д���������Ծ��꼶һ�ࡢ�����10��ѧ�����к�����д���ԣ��Ʒֲ���10���ƣ��÷־�ȡ���������ɼ��ﵽ6�ֻ�6������Ϊ���õ�9��Ϊ���㣬�ɼ����1��ʾ���������˳ɼ�����������2���� ��1
һ�� | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
���� | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
��2
�༶ | ƽ���� | ��λ�� | ���� | ���� | ������ | ������ |
һ�� | 7.6 | 8 | a | 3.82 | 70% | 30% |
���� | b | 7.5 | 10 | 4.94 | 80% | 40% |
��1���ڱ�2�У�a= �� b=��
��2������˵����ļ����ʡ������ʾ�����һ�࣬���Զ����һ��ã���Ҳ������Ϊһ��ɼ��ȶ���ã�����������һ��ɼ��õ��������ɣ�
��3��һ�ࡢ��������ֵ���ͬѧ�Ա�ֱ���1��1Ů��2��1Ů���ִ�����������ֵ�ͬѧ�и���1��ͬѧ�μӡ�������д������������״ͼ���б������ǡ�ó鵽1��1Ů��λͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x2��3|x��1|��4x��3��b��bΪ��������ͼ����x��ǡ�����������㣬����b��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���E�DZ�AD��һ�㣬��AE=2ED��EC���Խ���BD�ڵ�F���� ![]() ���ڣ� ��
���ڣ� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB�ǡ�O��ֱ����AT�ǡ�O�����ߣ���ABT=50�㣬BT����O�ڵ�C��E��AB��һ�㣬�ӳ�CE����O�ڵ�D��
��1����ͼ�٣����T�͡�CDB�Ĵ�С�� 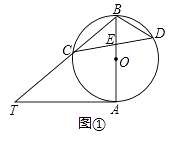
��2����ͼ�ڣ���BE=BCʱ�����CDO�Ĵ�С�� 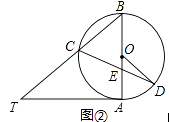
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com