
����Ŀ��ijУΪѡ��һ��ѡ�ֲμӡ������˳ǣ���Ϊ���������ԡ������ݽ����������о�������ͼ��ʾ����Ŀ��Ȩ����ѡ�����IJ���ѡ�ֽ��п��������Ű�ԭ��ͳ��ͼ����������
�±����������Ż���ѡ�����еĵ÷������
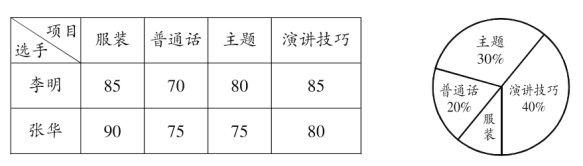
���������Ϣ���ش��������⣺
��1�����װ��Ŀ��Ȩ������ͨ����Ŀ��Ӧ���ε�Բ�ĽǴ�С��
��2����������ѡ�������ĸ���Ŀ���÷�������������λ����
��3����������ѧ��֪ʶ������ѧУ���������Ż�������ѡ��һ�˲μӡ������˳ǣ���Ϊ���������ԡ������ݽ���������˵�����ɣ�
���𰸡���1��10%��72�㣻��2��������85����λ����82.5����3��ѡ�������μӡ������˳ǣ���Ϊ���������ԡ������ݽ������������������
��������
��1���ȸ��ݸ������Ȩ��֮��Ϊ1����װ��Ŀ��Ȩ�����ٸ��ݸ�������������Բ�Ľ�=Ȩ��![]() ��⼴�ã�
��⼴�ã�
��2���ȸ��������Ķ��壬�ҳ��������÷����г��ִ������ķ��������������ٸ�����λ���Ķ��壬���������÷�����С������ߴӴ�С���У���ȡ�м���������ƽ����������λ����
��3���ȸ��ݸ���Ŀ�÷ּ�Ȩ���ֱ�����������Ż��ļ�Ȩƽ��������ѡȡƽ���ɼ��ߵ�ѡ�ּ��ã�
�⣺��1����װ��Ŀ��Ȩ����![]() ��
��
��ͨ����Ŀ��Ӧ���ε�Բ�Ľ���![]()
��2�����������ĸ���Ŀ���÷�����85�ֳ������Σ��������
��������ѡ�������ĸ���Ŀ���÷�����������85�֣�
��������ѡ�������ĸ���Ŀ���÷�����С��������Ϊ��70��80��85��85��
��������ѡ�������ĸ���Ŀ���÷�������λ����![]() ���֣�
���֣�
��3�������ĵ÷�Ϊ![]() ���֣�
���֣�
�Ż��ĵ÷�Ϊ![]() ���֣�
���֣�
��![]()
��������ƽ���ɼ��ã���ѡ�������μӡ������˳ǣ���Ϊ���������ԡ������ݽ�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������ԭ��O��x������ƽ��2����λ���ȵõ���A������A��y���ƽ���߽�����������![]() ��ͼ���ڵ�B��AB=
��ͼ���ڵ�B��AB=![]() ��
��
��1�����������Ľ���ʽ��
��2����P��![]() ��
�� ![]() ����Q��
����Q��![]() ��
�� ![]() ���Ǹ÷���������ͼ���ϵ����㣬��
���Ǹ÷���������ͼ���ϵ����㣬��![]() ʱ��
ʱ�� ![]() ��ָ����P��Q��λ���ĸ����ޣ�����Ҫ˵�����ɣ�
��ָ����P��Q��λ���ĸ����ޣ�����Ҫ˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA��OC�ֱ�λ��x�ᣬy���ϣ�����A��C����������߱�x������һ��D������AC������ֻ���̶ȵ�ֱ�߰�Ҫ��ͼ��
(1)��ͼ1�е��������ϣ�������E��ʹDE=AC��
(2)��ͼ2�е��������ϣ����������ߵĶ���F��
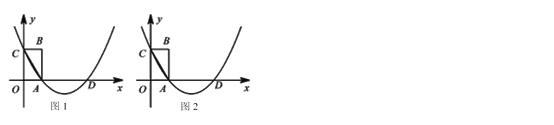
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ǰڷ����������Ի���ǰ�ļ�������Բ����ˮ�۴����濴����ͼ�Σ��ײ�����������ˮ���Ҳ�����һԲ�������飨Բ����������µ�����ȫ����ˮ�۵��棬����ĸ߶ȵ���ˮ�۵ĸ߶ȣ����������ײ��е�ˮ����ע���Ҳۣ�ͬʱ�Ի���ʱ��������������ǰѼס�������ˮ����ˮ�����![]() ��עˮʱ��
��עˮʱ��![]() ֮��Ĺ�ϵ��������ͼ��ʾ�ĺ���ͼ������ݺ���ͼ���ṩ����Ϣ������������⣺
֮��Ĺ�ϵ��������ͼ��ʾ�ĺ���ͼ������ݺ���ͼ���ṩ����Ϣ������������⣺
��1����ͼ��ʾ���߶�![]() ��ʾ ����ˮ�������עˮʱ��֮��Ĺ�ϵ������
��ʾ ����ˮ�������עˮʱ��֮��Ĺ�ϵ������![]() ��ʾ ����ˮ�������עˮʱ��֮��Ĺ�ϵ������������������ ��������������
��ʾ ����ˮ�������עˮʱ��֮��Ĺ�ϵ������������������ ��������������![]() ��������14��ʾ��ʵ�������� ��
��������14��ʾ��ʵ�������� ��
��2���ֱ����߶�![]() ���߶�
���߶�![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��3��עˮ�ʱ��ʱ���ס�������ˮ����ˮ�������ͬ��
��4������ˮ�۵ĵ����Ϊ![]() ��ˮ�۱ڵĺ�Ȳ��ƣ�������ˮ�������������Ƕ���
��ˮ�۱ڵĺ�Ȳ��ƣ�������ˮ�������������Ƕ���![]() ��
��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С����ѧ�õ����г����ͺ���24Ӣ�������ֵ�ֱ��Ϊ24Ӣ����Լ60���ף���Ϊ�˷�ֹ���������ﳵʱ����ˮ�������ϣ����������г����ֵ���Ӱ��������װ�ϵ�ˮ����Ƥ��������Ӱ���ֱַ�����C��DΪԲ�ĵ��������Σ��������ı���ABCD����DAB=125�㡢��ABC=115������ôԤ����Ҫ����Ƥ���Լ�ǣ�������

A. 942ƽ������ B. 1884ƽ������
C. 3768ƽ������ D. 4000ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ���װ��5��ֻ����ɫ��ͬ��������3������2������
��1����Ӵ���ͬʱ�������������ǻ���ĸ��ʣ�
��2���ֽ�����Ͱ������ɸ�����������ǰ��������2����������У����Ⱥ����Ӵ�������һ�����Ǻ���ĸ�����![]() ���������еĺ���ĸ�����
���������еĺ���ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=��a��1��x2+3x��6��ͼ����x��Ľ���ΪA��B������Bһ��������ԭ��ͣ�1��0��֮�䣬��B�㲻��ԭ��ͣ�1��0���غϣ���ôa��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����˽̰���꼶�ϲ���ѧ�̲�P53����ѧ���������һ�����������ı���ABCD�У���AD=CD��AB=CB�������ǰ����������ڱ߷ֱ���ȵ��ı��ν��������������Բ������εĽǣ��Խ�����ʲô���ʣ�Ȼ��ѡ������һ��������ȫ�������ε�֪ʶ֤����IJ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����BAC��90�㣬��D���߶�BC�ϣ���EDB��![]() ��C��BE��DE������ΪE��DE��AB�ཻ�ڵ�F.��̽���߶�BE��DF��������ϵ����֤����Ľ��ۣ�
��C��BE��DE������ΪE��DE��AB�ཻ�ڵ�F.��̽���߶�BE��DF��������ϵ����֤����Ľ��ۣ�
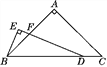
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com