
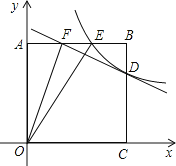
【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线![]() 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
【答案】(1)y=![]() ;(2)点F的坐标为(2,4).(3)∠AOF=∠EOC.见解析
;(2)点F的坐标为(2,4).(3)∠AOF=∠EOC.见解析
【解析】试题分析:(1)设反比例函数的解析式为y=,把点E(3,4)代入即可求出k的值,进而得出结论;
(2)由正方形AOCB的边长为4,故可知点D的横坐标为4,点F的纵坐标为4.由于点D在反比例函数的图象上,所以点D的纵坐标为3,即D(4,3),由点D在直线y=﹣x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标;
(3)在CD上取CG=AF=2,连接OG,连接EG并延长交x轴于点H,由全等三角形的判定定理可知△OAF≌△OCG,△EGB≌△HGC(ASA),故可得出EG=HG.设直线EG的解析式为y=mx+n,把E(3,4),G(4,2)代入即可求出直线EG的解析式,故可得出H点的坐标,在Rt△AOF中,AO=4,AE=3,根据勾股定理得OE=5,可知OH=OE,即OG是等腰三角形底边EF上的中线.所以OG是等腰三角形顶角的平分线,由此即可得出结论.
解:(1)设反比例函数的解析式y=,
∵反比例函数的图象过点E(3,4),
∴4=,即k=12.
∴反比例函数的解析式y=![]() ;
;
(2)∵正方形AOCB的边长为4,
∴点D的横坐标为4,点F的纵坐标为4.
∵点D在反比例函数的图象上,
∴点D的纵坐标为3,即D(4,3).
∵点D在直线y=﹣x+b上,
∴3=﹣×4+b,解得b=5.
∴直线DF为y=﹣x+5,
将y=4代入y=﹣x+5,得4=﹣x+5,解得x=2.
∴点F的坐标为(2,4).
(3)∠AOF=∠EOC.
证明:在CD上取CG=AF=2,连接OG,连接EG并延长交x轴于点H.
∵AO=CO=4,∠OAF=∠OCG=90°,AF=CG=2,
∴△OAF≌△OCG(SAS).
∴∠AOF=∠COG.
∵∠EGB=∠HGC,∠B=∠GCH=90°,BG=CG=2,
∴△EGB≌△HGC(ASA).
∴EG=HG.
设直线EG:y=mx+n,
∵E(3,4),G(4,2),
∴![]() ,解得,
,解得,![]() .
.
∴直线EG:y=﹣2x+10.
令y=﹣2x+10=0,得x=5.
∴H(5,0),OH=5.
在Rt△AOE中,AO=4,AE=3,根据勾股定理得OE=5.
∴OH=OE.
∴OG是等腰三角形底边EH上的中线.
∴OG是等腰三角形顶角的平分线.
∴∠EOG=∠GOH.
∴∠EOG=∠GOC=∠AOF,即∠AOF=∠EOC.
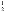


科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程x2﹣4x+m+1=0有两个不相等的实数根.
(1)求m的取值范围;(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解该校学生的课余活动情况,抽样调查了部分同学,将所得数据处理后,制成折线统计图(部分)和扇形统计图(部分)如下:
(1)在这次研究中,一共调查了 名学生.
(2)补全频数分布折线图;
(3)该校共有2200名学生,估计该校学生中爱好阅读的人数大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
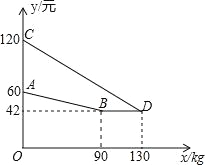
(1)求线段AB所表示的y1与x之间的函数表达式;线段CD所表示的y2与x之间的函数表达式.
(2)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com