练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某宾馆有120间标准房，当每间标准房每天价格为100元时，每天都客满，市场调查表明每间标准房每天价格在100~180元之间（含100元，180元）浮动时，每提高5元，日均入住数减少3间，每间标准房如果有人入住每天各种费用40元，如果没人入住每天需各种费用10元，宾馆将每间标准房每天价格提高到多少元时，客房的日收益额最大？（注：收益额营业收入各种费用）

    【答案】宾馆将每间标准房每天价格提高到165元时，客房的日收益额最大．

    【解析】

    首先设宾馆客房租金每间日租金为x元，以及客房租金收入为y，建立y与x的关系式，并通过二次函数求解最大值．

    解：设每间标准房每天价格为元，客房的日收益额为元，由题意，得

    ，

    化简，得：；

    ∵，

    ∵，

    ∵在范围内，

    ∴当时，客房的日收益额最大．

    答：宾馆将每间标准房每天价格提高到165元时，客房的日收益额最大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在我国新型冠状病毒防控形势好转的态势下，各行各业复工复产所需的“消杀防护”设备成为急需物品．某医药超市库存的甲，乙两种型号“消杀防护”套装共套全部售完，售后统计甲型号套装每套的利润为元，乙型号套装每套的利润为元，两种型号“消杀防护"套装售完后的总利润为元

    请计算本次销售中甲、乙两种型号“消杀防护”套装各销售了多少套．

    由于企业迫切需求，该医药超市决定再次购进套甲、乙两种型号的“消杀防护”套装，商场规定甲型号套装的采购数量不得超过乙型号的倍，请你通过计算说明如何采购才能让第二次销售获得最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

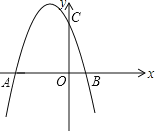
    【题目】如图，抛物线y＝ax2+bx+3与x轴交于A（﹣3，0），B（l，0）两点，与y轴交于点C．

    （1）求抛物线的解析式；

    （2）点P是抛物线上的动点，且满足S△PAO＝2S△PCO，求出P点的坐标；

    （3）连接BC，点E是x轴一动点，点F是抛物线上一动点，若以B、C、E、F为顶点的四边形是平行四边形时，请直接写出点F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

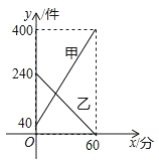
    【题目】某快递公司每天上午9：00－10：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，那么当两仓库快递件数相同时，此刻的时间为__________；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个箱子内有3颗相同的球，将3颗球分别标示号码1，2，5，今浩浩以每次从箱子内取一颗球且取后放回的方式抽取，并预计取球10次，现已取了8次，取出的结果依次为1，2，2，5，5，2，1，2，若每次取球时，任一颗球被取到的机会皆相等，且取出的号码即为得分数，浩浩打算依计划继续从箱子取球2次，则发生“这10次得分的平均数在2.2~2.4之间（含2.2，2.4）”的情形的概率为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抚顺市某校想知道学生对“遥远的赫图阿拉”，“旗袍故里”等家乡旅游品牌的了解程度，随机抽取了部分学生进行问卷调查，问卷有四个选项（每位被调查的学生必选且只选一项）A．十分了解，B．了解较多，C．了解较少，D．不知道．将调查的结果绘制成如下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：

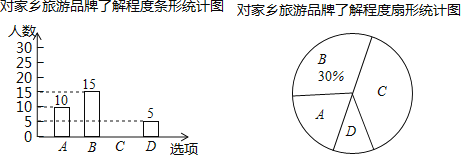
    （1）本次调查了多少名学生？

    （2）补全条形统计图；

    （3）该校共有500名学生，请你估计“十分了解”的学生有多少名？

    （4）在被调查“十分了解”的学生中有四名学生会干部，他们中有3名男生和1名女生，学校想从这4人中任选两人做家乡旅游品牌宣传员，请用列表或画树状图法求出被选中的两人恰好是一男一女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知将抛物线沿轴向上翻折与所得抛物线围成一个封闭区域（包括边界），在这个区域内有5个整点（点满足横、纵坐标都为整数，则把点叫做“整点”）.现将抛物线沿轴向下翻折，所得抛物线与原抛物线所围成的封闭区域内（包括边界）恰有11个整点，则的取值范围是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P是AB边上的动点(不与点B重合)将△BCP沿CP所在的直线翻折，得到，连接，下面有四个判断：

    ①当AP=BP时，∥CP；

    ②当AP=BP时，

    ③当CP⊥AB时，；

    ④长度的最小值是1．

    所有正确结论的序号是( )

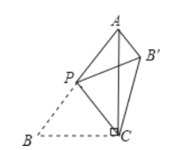
    A.①③④B.①②C.①②④D.②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明对函数的图象和性质进行了探究．已知当自变量的值为1时，函数值为4；当自变量的值为2时，函数值为3；探究过程如下，请补充完整：

    （1）求这个函数的表达式；

    （2）在给出的平面直角坐标系中，画出这个函数的图象并写出这个函数的一条性质： ；

    （3）进一步探究函数图象并解决问题：已知函数的图象如图所示，结合你所画的函数图象，写出不等式的解集： ．

    查看答案和解析>>

    同步练习册答案