
| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
分析 根据等腰三角形三线合一的性质知:若过A作BC的垂线,设垂足为D,则AD必垂直平分BC;由垂径定理可知,AD必过圆心O;根据等腰直角三角形的性质,易求出BD、AD的长,进而可求出OD的值;连接OB根据勾股定理即可求出⊙O的半径.
解答 解:过A作AD⊥BC,由题意可知AD必过点O,连接OB;
∵△BAC是等腰直角三角形,AD⊥BC,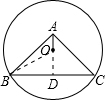
∴BD=CD=AD=3;
∴OD=AD-OA=2;
Rt△OBD中,根据勾股定理,得:
OB=$\sqrt{B{D}^{2}+O{D}^{2}}$=$\sqrt{13}$.
故选C.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
| 小明家 | 爷爷家 | |
| 屋顶收集雨水面积(m2) | 160 | 120 |
| 蓄水池容积(m3) | 50 | 13 |
| 蓄水池已有水量(m3) | 34 | 11.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 增加6m2 | B. | 减少6m2 | C. | 增加9m2 | D. | 减少9m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
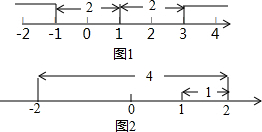
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:解答题
在直角坐标系中,△ABC的三个顶点的位置如图所示.
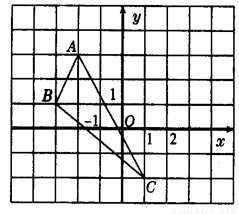
(1)请画出将△ABC先向右平移3个单位,再向上平移1个单位后得△A′B′C′,请在网格纸中画出△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′、B′、C′三点的坐标:A′_____,B′______,C′______.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:单选题
若点P( ,
,  )在第二象限,则k的取值范围是( )
)在第二象限,则k的取值范围是( )
A.  <
<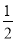 B.
B. 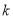 <2 C.
<2 C. 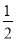 <
<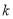 <2 D.
<2 D. 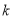 >2
>2
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
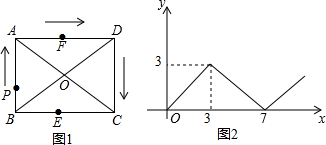 如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )| A. | 点C | B. | 点F | C. | 点D | D. | 点O |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com