练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
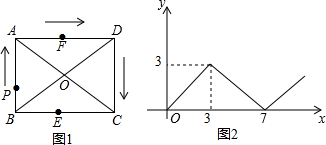
    10．如图，矩形ABCD中，对角线AC，BD交于点O，E，F分别是边BC，AD的中点，AB=3，BC=4，一动点P从点B出发，沿着B-A-D-C在矩形的边上运动，运动到点C停止，点M为图1中某一定点，设点P运动的路程为x，△BPM的面积为y，表示y与x的函数关系的图象大致如图2所示．则点M的位置可能是图1中的（　　）
    A．点CB．点FC．点DD．点O

    分析 从图2中可看出当x=7时，此时△BPM的面积为0，说明点M一定在BD上，选项中有点O和D在BD上，此时x=3，y=3，所以点M的位置是图1中的点O．

    解答 解：∵AB=3，BC=4，四边形ABCD是矩形，
    ∴当x=7时，点P到达D点，此时△BPM的面积为0，说明点M一定在BD上，
    ∵x=3，y=3，
    ∴从选项中可得只有O点符合，所以点M的位置是图1中的点O．
    故选：D．

    点评 本题主要考查了动点问题的函数图象，解题的关键是找出当x=7时，此时△BPM的面积为0，说明点M一定在BD上这一信息．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．⊙O过点B，C，圆心O在等腰直角△ABC内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（　　）
    A．$\sqrt{10}$B．2$\sqrt{3}$C．$\sqrt{13}$D．3$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷（解析版） 题型：填空题

    已知，那么=_______。

    查看答案和解析>>

    科目：初中数学 来源：2017届湖北省赤壁市九年级下学期第一次模拟（调研）考试数学试卷（解析版） 题型：解答题

    阅读理【解析】
    运用“同一图形的面积相等”可以证明一些含有线段的等式成立，这种解决问题的方法我们称之为面积法. 如图1，在等腰△ABC中，AB=AC， AC边上的高为h，点M为底边BC上的任意一点，点M到腰AB、AC的距离分别为h1、h2，连接AM，利用S△ABC=S△ABM＋S△ACM，可以得出结论：h= h1＋h2.

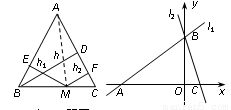
    类比探究：在图1中，当点M在BC的延长线上时，猜想h、h1、h2之间的数量关系并证明你的结论.

    拓展应用：如图2，在平面直角坐标系中，有两条直线l1：y =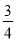x+3，l2：y =－3x+3，若l2上一点M到l1的距离是1，试运用 “阅读理解”和“类比探究”中获得的结论，求出点M的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

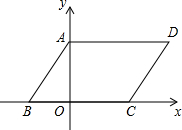    6．如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD=6，若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根，且OA＞OB．
    （1）求OA、OB的长；
    （2）若点E为x轴上的点，且S△AOE=$\frac{16}{3}$，求出点E的坐标；
    （3）判断△AOE与△AOD是否相似？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

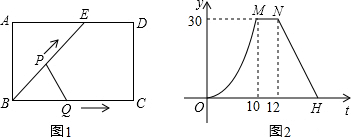    14．如图1，点E为矩形ABCD的边AD上一点，点P、点Q同时从点B出发，点P沿BE→ED→DC 运动到点C停止，点Q沿BC运动到点C停止，它们运动的速度都是1cm/s，设P、Q出发t秒时，△BPQ的面积为ycm2，已知y与t的函数关系如图2（曲线OM为抛物线的一部分），则下列结论：
    ①AB=6cm；
    ②当0＜t≤10时，y=$\frac{3}{10}$t2；
    ③NH所在直线的解析式为y=-5t+90；
    ④sin∠PBQ=$\frac{1}{2}$时，t=13秒．
    其中错误的结论个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

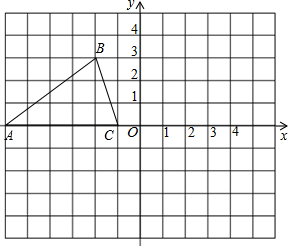    1．如图，已知△ABC的三个顶点的坐标分别为A（-6，0）、B（-2，3）、C（-1，0）．
    （1）将△ABC绕坐标原点O逆时针旋转90°．画出对应的△A′B′C′图形；
    （2）若四边形A′B′C′D′为平行四边形，请直接写出第四个顶点D′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．
    （1）求商场经营该商品原来一天可获利润2000元．
    （2）设后来该商品每件降价x元，商场一天可获利润y元．
    ①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？
    ②求出y与x之间的函数关系式，当x取何值时，商场获利润最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．解分式方程：$\frac{12}{{x}^{2}-9}$+$\frac{2}{3-x}$=0．

    查看答案和解析>>

    同步练习册答案