
阅读理【解析】
运用“同一图形的面积相等”可以证明一些含有线段的等式成立,这种解决问题的方法我们称之为面积法. 如图1,在等腰△ABC中,AB=AC, AC边上的高为h,点M为底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2,连接AM,利用S△ABC=S△ABM+S△ACM,可以得出结论:h= h1+h2.
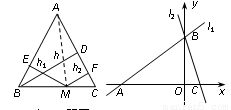
类比探究:在图1中,当点M在BC的延长线上时,猜想h、h1、h2之间的数量关系并证明你的结论.
拓展应用:如图2,在平面直角坐标系中,有两条直线l1:y =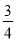 x+3,l2:y =-3x+3,若l2上一点M到l1的距离是1,试运用 “阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
x+3,l2:y =-3x+3,若l2上一点M到l1的距离是1,试运用 “阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:单选题
若点P( ,
,  )在第二象限,则k的取值范围是( )
)在第二象限,则k的取值范围是( )
A.  <
<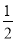 B.
B. 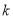 <2 C.
<2 C. 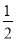 <
<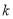 <2 D.
<2 D. 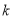 >2
>2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
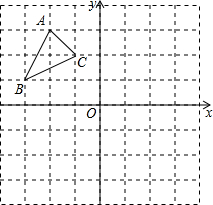 如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).
如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
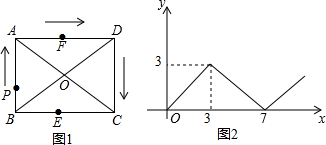 如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )| A. | 点C | B. | 点F | C. | 点D | D. | 点O |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
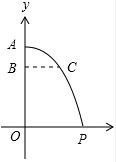 2008年7月某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口A,如图所示,如果空投物资离开A处后下落的垂直高度AB=160米时,它测A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为500米.
2008年7月某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口A,如图所示,如果空投物资离开A处后下落的垂直高度AB=160米时,它测A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为500米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
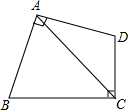 如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是20cm2,则AC的长是2$\sqrt{10}$cm.
如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是20cm2,则AC的长是2$\sqrt{10}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com