
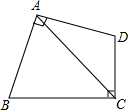
 如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是20cm2,则AC的长是2$\sqrt{10}$cm.
如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是20cm2,则AC的长是2$\sqrt{10}$cm. 分析 作AE⊥BC于E,作AF⊥CD,交CD的延长线于点F,得出四边形AECF为矩形,由矩形性质得出∠EAF为直角,证出∠DAF=∠BAE,由AAS证明△ABE≌△ADF,得出AE=AF,证出四边形AECF为正方形,△ABE面积与△AFD面积相等,得出四边形ABCD面积等于正方形AECF面积,求出正方形边长AE的长,再运用等腰直角三角形的性质即可求出AC的长.
解答 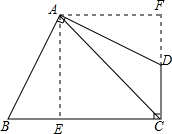 解:作AE⊥BC于E,作AF⊥CD,交CD的延长线于点F,
解:作AE⊥BC于E,作AF⊥CD,交CD的延长线于点F,
则∠AEC=∠F=∠ECF=90°,
∴四边形AECF为矩形,
∴∠EAF=90°,
∵∠BAD=90°,
∴∠BAE+∠EAD=∠FAD+∠EAD=90°,
∴∠DAF=∠BAE,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{∠AEB=∠F=90°}&{\;}\\{∠BAE=∠DAF}&{\;}\\{AB=AD}&{\;}\end{array}\right.$,
∴△ABE≌△ADF(AAS),
∴AE=AF,S△ABE=S△ADF,
∴四边形AECF是正方形,
∴S四边形ABCD=S正方形AECF=20cm2,
∴AE=2$\sqrt{5}$cm,
∵△AEC为等腰直角三角形,
∴AC=$\sqrt{2}$AE=2$\sqrt{10}$cm.
故答案为:2$\sqrt{10}$.
点评 本题考查了全等三角形的判定与性质、正方形的判定与性质、矩形的判定与性质;熟练掌握全等三角形的判定与性质,通过作正方形构造三角形全等证出正方形是解决问题的关键.


科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
阅读理【解析】
运用“同一图形的面积相等”可以证明一些含有线段的等式成立,这种解决问题的方法我们称之为面积法. 如图1,在等腰△ABC中,AB=AC, AC边上的高为h,点M为底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2,连接AM,利用S△ABC=S△ABM+S△ACM,可以得出结论:h= h1+h2.
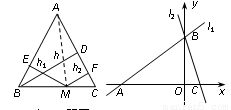
类比探究:在图1中,当点M在BC的延长线上时,猜想h、h1、h2之间的数量关系并证明你的结论.
拓展应用:如图2,在平面直角坐标系中,有两条直线l1:y =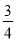 x+3,l2:y =-3x+3,若l2上一点M到l1的距离是1,试运用 “阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
x+3,l2:y =-3x+3,若l2上一点M到l1的距离是1,试运用 “阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
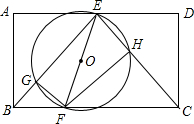 如图,矩形ABCD中,E为AD中点,点F为BC上的动点(不与B、C重合).连接EF,以EF为直径的圆分别交BE,CE于点G、H.设BF的长度为x,弦FG与FH的长度和为y,则下列图象中,能表示y与x之间的函数关系的图象大致是( )
如图,矩形ABCD中,E为AD中点,点F为BC上的动点(不与B、C重合).连接EF,以EF为直径的圆分别交BE,CE于点G、H.设BF的长度为x,弦FG与FH的长度和为y,则下列图象中,能表示y与x之间的函数关系的图象大致是( )| A. | 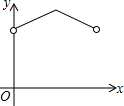 | B. | 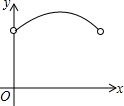 | C. | 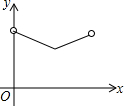 | D. | 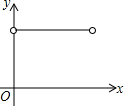 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
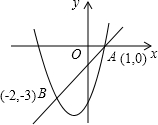 如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,0),B(-2,-3)两点,若y1>y2,则x的取值范围是( )
如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,0),B(-2,-3)两点,若y1>y2,则x的取值范围是( )| A. | x<-2 | B. | -2<x<1 | C. | x>1 | D. | x<-2或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 早晨,小刚沿着通往学校唯一的一条路(直线)上学,途中发现忘带盒饭,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
早晨,小刚沿着通往学校唯一的一条路(直线)上学,途中发现忘带盒饭,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com