
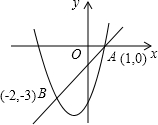
 如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,0),B(-2,-3)两点,若y1>y2,则x的取值范围是( )
如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,0),B(-2,-3)两点,若y1>y2,则x的取值范围是( )| A. | x<-2 | B. | -2<x<1 | C. | x>1 | D. | x<-2或x>1 |
科目:初中数学 来源: 题型:解答题
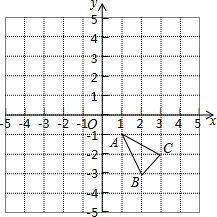 在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).
在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
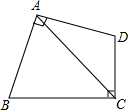 如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是20cm2,则AC的长是2$\sqrt{10}$cm.
如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是20cm2,则AC的长是2$\sqrt{10}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
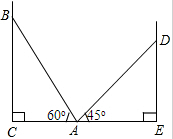 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,DE=3$\sqrt{2}$m,求BC的长度.
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,DE=3$\sqrt{2}$m,求BC的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 今年某市遭遇干旱,为鼓励市民节约用水,该市自来水公司按分段收费标准收费,如图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.
今年某市遭遇干旱,为鼓励市民节约用水,该市自来水公司按分段收费标准收费,如图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com