
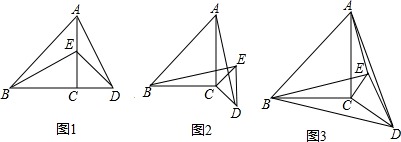
分析 (1)①由CA=CB,CE=CD,∠ACB=90°易证△BCE≌△ACD,所以BE=AD,∠BEC=∠ADC,又因为∠EBC+∠BEC=90°,所以∠EBC+∠ADC=90°,即BE⊥AD;
②成立.设BE与AC的交点为点F,BE与AD的交点为点G,易证△ACD≌△BCE.得到AD=BE,∠CAD=∠CBE.再根据等量代换得到∠AFG+∠CAD=90°.即BE⊥AD;
(2)易证△ACD∽△BCE.得到∠CAD=∠CBE.再根据等量代换得到∠AFG+∠CAD=90°,即BE⊥AD,根据勾股定理得到BD2+AE2=AB2+ED2,即可根据勾股定理计算.
解答 (1)①BE=AD,BE⊥AD;
证明:在△BCE和△ACD中,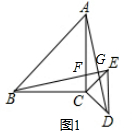
$\left\{\begin{array}{l}{CA=CB}\\{∠ACB=∠ACD=90°}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD,
∴BE=AD,∠BEC=∠ADC,
∵∠EBC+∠BEC=90°,
∴∠EBC+∠ADC=90°,
∴BE⊥AD.
②BE=AD,BE⊥AD仍然成立;
证明:设BE与AC的交点为点F,BE与AD的交点为点G,如图1.
∵∠ACB=∠ECD=90°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
$\left\{\begin{array}{l}AC=BC\\∠ACD=∠BCE\\ CD=CE\end{array}\right.$
∴△ACD≌△BCE.
∴AD=BE,∠CAD=∠CBE.
∵∠BFC=∠AFG,∠BFC+∠CBE=90°,
∴∠AFG+∠CAD=90°.
∴∠AGF=90°.
∴BE⊥AD.
(2)证明:设BE与AC的交点为点F,BE的延长线与AD的交点为点G,如图2.
∵∠ACB=∠ECD=90°
∴∠ACD=∠BCE.
∵CA=8,CB=6,CE=3,CD=4,
∴$\frac{CA}{CB}=\frac{CD}{CE}=\frac{4}{3}$.
∴△ACD∽△BCE.
∴∠CAD=∠CBE.
∵∠BFC=∠AFG,∠BFC+∠CBE=90°,
∴∠AFG+∠CAD=90°.
∴∠AGF=90°.
∴BG⊥AD.
∴∠AGE=∠BGD=90°.
∴AE2=AG2+EG2,BD2=BG2+DG2.
∴BD2+AE2=AG2+EG2+BG2+DG2.
∵AG2+BG2=AB2,EG2+DG2=ED2,
∴BD2+AE2=AB2+ED2=CA2+CB2+CD2+CE2=125.
点评 本题属于几何综合变换题,主要考查了图形的旋转变换、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理的综合运用,运用类比,在变化中发现规律是解决问题的关键.


科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
若(x+m)(x-8)中不含x的一次项,则m的值为( )
A. 8 B. -8 C. 0 D. 8或-8
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
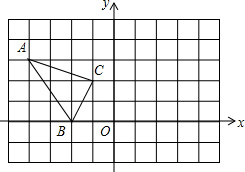 在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.
在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
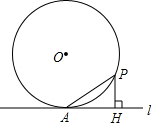 如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )
如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )| A. | 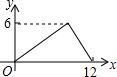 | B. | 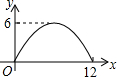 | C. | 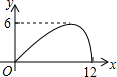 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
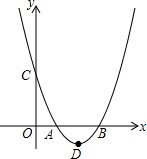 在平面直角坐标系中,抛物线y1=ax2-4ax+n与x轴的交点A、B,抛物线的顶点为D.
在平面直角坐标系中,抛物线y1=ax2-4ax+n与x轴的交点A、B,抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
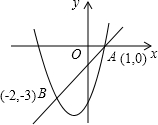 如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,0),B(-2,-3)两点,若y1>y2,则x的取值范围是( )
如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,0),B(-2,-3)两点,若y1>y2,则x的取值范围是( )| A. | x<-2 | B. | -2<x<1 | C. | x>1 | D. | x<-2或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
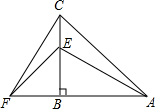 在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.
在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2015a>-2015b | B. | $\frac{1}{2}$a<0.5b | C. | 2015-a>2015-b | D. | a-2015>b-2015 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com