
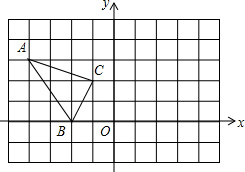
 在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.
在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.分析 (1)分别作出点A、B、C绕点O顺时针旋转90°后得到点,然后顺次连接;
(2)根据直角坐标系的特点写出点A′、B′、C′的坐标;
(3)用△ABC所在的矩形的面积减去三个小三角形的面积即可求解.
解答 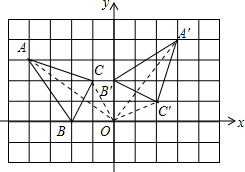 解:(1)所作图形如图所示:
解:(1)所作图形如图所示:
(2)A′(3,4)、B′(0,2)、C′(2,1);
(3)S△ABC=3×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3
=9-3-1-$\frac{3}{2}$
=$\frac{7}{2}$.
点评 本题考查了根据旋转变换作图,解答本题的关键是根据网格结构找出各点对应点的位置,然后顺次连接.


科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:填空题
已知等腰三角形的顶角为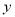 度,底角为
度,底角为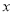 度,请写出顶角
度,请写出顶角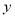 (度)与底角
(度)与底角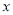 (度)之间的函数关系式__________________ ,自变量
(度)之间的函数关系式__________________ ,自变量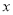 的取值范围是_____________;
的取值范围是_____________;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
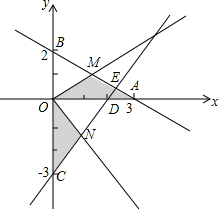 已知直线y=-$\frac{2}{3}$x+2分别与x轴、y轴相交于A、B两点,过点C(0,-3)作直线AB的垂线交直线AB于点E,交x轴于点D.
已知直线y=-$\frac{2}{3}$x+2分别与x轴、y轴相交于A、B两点,过点C(0,-3)作直线AB的垂线交直线AB于点E,交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
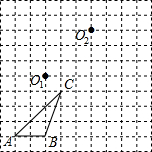 如图,网格中每个小正方形的边长均为1个单位长度
如图,网格中每个小正方形的边长均为1个单位长度查看答案和解析>>
科目:初中数学 来源: 题型:解答题
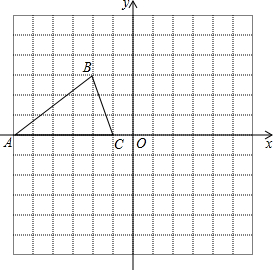 如图,已知△ABC的三个顶点坐标分别为A(-6,0)、B(-2,3)、C(-1,0).
如图,已知△ABC的三个顶点坐标分别为A(-6,0)、B(-2,3)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
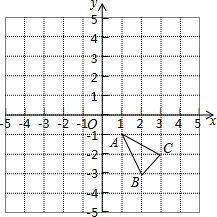 在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).
在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).
如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
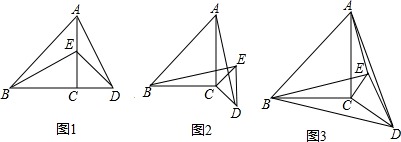
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com