
 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).
如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,3),B(0,5).分析 (1)根据旋转的性质得出对应点位置,进而得出答案;
(2)根据中心对称的性质得出对应点位置,进而得出答案;
(3)∠OAB=45°,根据A1(-3,6),A(6,3),可根据勾股定理求出OA=OA1=3$\sqrt{5}$,又∠AOA1=90°,易证△A1AO为等腰直角三角形,得∠OAB=45°.
解答 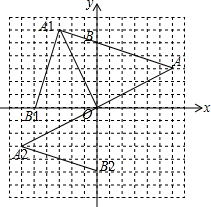 解:(1)如图所示,△OA1B1即为所求;
解:(1)如图所示,△OA1B1即为所求;
(2)如图所示△OA2B2即为所求;
(3)∠OAB=45°,
理由:∵A1(-3,6),A(6,3)
∴OA=OA1=3$\sqrt{5}$,
又∵∠AOA1=90°,
∴△A1AO为等腰直角三角形,
∴∠OAB=45°.
点评 此题主要考查了图形的旋转、中心对称以及勾股定理,得出旋转后对应点位置是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:单选题
根据分式的基本性质,分式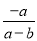 可变形为( )
可变形为( )
A. 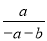 B.
B. 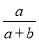 C.
C. 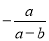 D.
D. 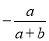
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
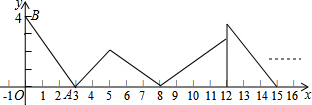
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
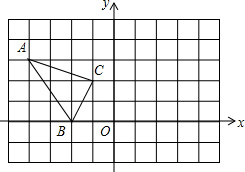 在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.
在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
(1)计算:4sin60°-︱3-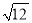 ︱+(
︱+(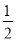 )-2;
)-2;
(2)解方程x2-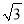 x-
x-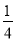 = 0.
= 0.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
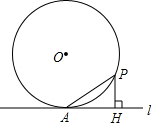 如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )
如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )| A. | 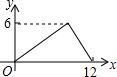 | B. | 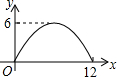 | C. | 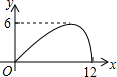 | D. | 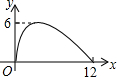 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
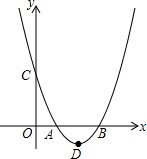 在平面直角坐标系中,抛物线y1=ax2-4ax+n与x轴的交点A、B,抛物线的顶点为D.
在平面直角坐标系中,抛物线y1=ax2-4ax+n与x轴的交点A、B,抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
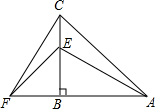 在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.
在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 累计购物 | 1300 | 2900 | … | x |
| 在甲商场实际花费 | 1270 | 2710 | … | 0.9x+100 |
| 在乙商场实际花费 | 1260 | 2780 | … | 0.95x+25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com