
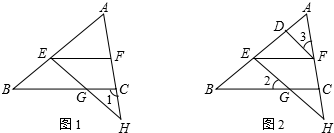
分析 (1)由条件可证明∠AFE=∠CFE,根据平行线的判定可证明BC∥EF;
(2)由条件可先证明DF∥EH,可得∠DFE=∠FEG,再结合(1)的结论和已知条件可证明∠3=∠DFE,可证得结论.
解答 证明:(1)∵∠1+∠AFE=180°,∠1+∠CFE=180°,
∴∠AFE=∠CFE,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.


科目:初中数学 来源: 题型:选择题
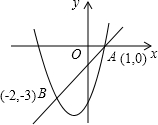 如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,0),B(-2,-3)两点,若y1>y2,则x的取值范围是( )
如图,二次函数y1=ax2+bx+c和一次函数y2=kx+b的图象交于A(1,0),B(-2,-3)两点,若y1>y2,则x的取值范围是( )| A. | x<-2 | B. | -2<x<1 | C. | x>1 | D. | x<-2或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).
已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
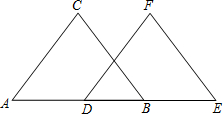 看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF
看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com