
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(3)方程利用配方法求出解即可;
(4)方程利用因式分解法求出解即可.
解答 解:(1)去分母得:x+2x-4=x+2,
解得:x=3,
经检验x=3是分式方程的解;
(2)去分母得:x-8+1=8x-56,
解得:x=7,
经检验x=7是增根,分式方程无解;
(3)方程整理得:x2-2x=$\frac{1}{2}$,
配方得:x2-2x+1=$\frac{3}{2}$,即(x-1)2=$\frac{3}{2}$,
开方得:x-1=±$\frac{\sqrt{6}}{2}$,
解得:x1=1+$\frac{\sqrt{6}}{2}$,x2=1-$\frac{\sqrt{6}}{2}$;
(4)分解因式得:(x-2$\sqrt{2}$)2=0,
开方得:x1=x2=2$\sqrt{2}$.
点评 此题考查了解分式方程,以及解一元二次方程-配方法,熟练掌握运算法则是解本题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
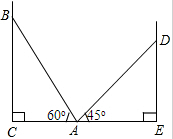 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,DE=3$\sqrt{2}$m,求BC的长度.
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,DE=3$\sqrt{2}$m,求BC的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2-4(a+b)+4=(a+b-2)2 | B. | (y+5)(y-5)=y2-25 | ||
| C. | x2+2x+1=x(x+2)+1 | D. | -18x4y3=-6x2y2•3x2y |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①和② | B. | ①③和④ | C. | ②和③ | D. | ②③和④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com