
| A. | ①和② | B. | ①③和④ | C. | ②和③ | D. | ②③和④ |
分析 由“一组对边平行且相等的四边形是平行四边形”得出①不正确;
由平行线的性质和添加条件得出AD∥BC,得出四边形ABCD是平行四边形,②正确;
由平行线得出△AOB∽△COD,得出对应边成比例,证出BO=DO,得出四边形ABCD是平行四边形,③正确;
先证出AO=BO,在证明△AOB∽△COD,得出对应边成比例得出CO=DO,因此四边形ABCD不一定是平行四边形,得出④不正确.
解答 解:∵一组对边平行且相等的四边形是平行四边形,
∴①不正确;
∵AB∥CD,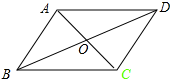
∴∠ABC+∠BCD=180°,
∵∠BAD=∠BCD,
∴∠ABC+∠BAD=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,
∴②正确,如图所示;
∵AB∥CD,
∴△AOB∽△COD,
∴AO:CO=BO:DO,
∵AO=CO,
∴BO=DO,
∴四边形ABCD是平行四边形,
∴③正确;
∵∠DBA=∠CAB,
∴AO=BO,
∵AB∥CD,
∴△AOB∽△COD,
∴AO:CO=BO:DO,
∵AO=BO,
∴CO=DO,四边形ABCD不一定是平行四边形,
∴④不正确;
故选:C.
点评 本题考查了平行四边形的判定、平行线的性质、相似三角形的判定与性质;熟练掌握平行四边形的判定方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).
已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
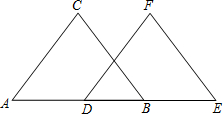 看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF
看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
已知关于x的方程kx2+(k+2) x+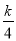 =0有两个不相等的实数根,则k的取值范围是__________.
=0有两个不相等的实数根,则k的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com