
 已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).
已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).分析 (1)利用待定系数法,把A、B两点坐标代入可求得a、b的值,可求得一次函数解析式;
(2)把x=-5代入函数解析式,可求得对应的函数y的值;
(3)结合函数图象可知当x≥0时,即对应的函数图象在y轴右侧的部分,可写出对应的y的取值范围.
解答 解:
(1)∵函数图象过A、B两点,
∴把A、B两点的坐标代入解析式可得$\left\{\begin{array}{l}{2a+b=0}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-2}\\{b=4}\end{array}\right.$,
∴一次函数解析式为y=-2x+4,
其图象如图所示: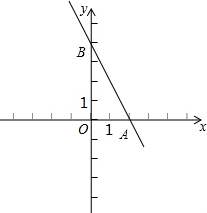
(2)当x=-5时,y=-2×(-5)+4=14,
∴当x=-5时,对应的y值为14;
(3)当x≥0时,对应的函数图象在y轴的右侧,结合图象可知此时y≤4.
点评 本题主要考查待定系数法求函数解析式,掌握待定系数法求函数解析式的方法是解题的关键,注意数形结合.


科目:初中数学 来源: 题型:解答题
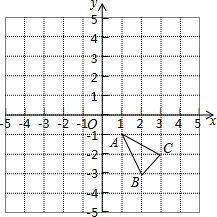 在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).
在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
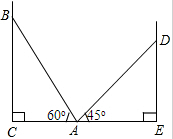 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,DE=3$\sqrt{2}$m,求BC的长度.
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,DE=3$\sqrt{2}$m,求BC的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 今年某市遭遇干旱,为鼓励市民节约用水,该市自来水公司按分段收费标准收费,如图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.
今年某市遭遇干旱,为鼓励市民节约用水,该市自来水公司按分段收费标准收费,如图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①和② | B. | ①③和④ | C. | ②和③ | D. | ②③和④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com