
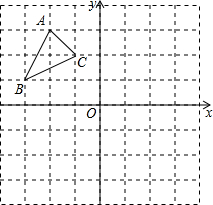
 如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).
如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).分析 (1)利用平移的性质得出对应点位置进而得出答案;
(2)利用轴对称图形的性质得出对应点位置进而得出答案;
(3)利用旋转的性质得出对应点位置进而得出答案;
(4)利用所画图形进而分析得出即可.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)如图所示:△A3 B3C3,即为所求;
(4)与△A3 B3C3成轴对称的图形是△A2B2C2,对称轴是y轴;
与△A1B1C1成中心对称的图形是△A3B3C3.
故答案为:△A2B2C2,y轴,△A3B3C3.
点评 此题主要考查了轴对称变换、旋转变换和平移变换,根据题意得出对应点位置是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
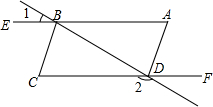 如图,AE∥CF,∠A=∠C.
如图,AE∥CF,∠A=∠C.查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
认真阅读材料,然后回答问题:我们初中学习了多项式的运算法则,相应的我们可以计算出多项式的展开式,如:(a+b)1=a+b,
(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,…下面我们依次对(a+b)n展开式的各项系数进一步研究发现,当n取正整数是可以单独列成表中的形式: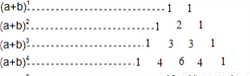
上面的多项式展开系数表称为“杨辉三角形”;仔细观察“杨辉三角形”,用你发现的规律回答下列问题:(1)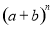 展开式中共有多少项?
展开式中共有多少项?
(2)请写出多项式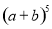 的展开式?
的展开式?
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
阅读理【解析】
运用“同一图形的面积相等”可以证明一些含有线段的等式成立,这种解决问题的方法我们称之为面积法. 如图1,在等腰△ABC中,AB=AC, AC边上的高为h,点M为底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2,连接AM,利用S△ABC=S△ABM+S△ACM,可以得出结论:h= h1+h2.
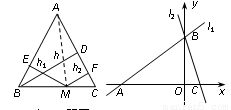
类比探究:在图1中,当点M在BC的延长线上时,猜想h、h1、h2之间的数量关系并证明你的结论.
拓展应用:如图2,在平面直角坐标系中,有两条直线l1:y =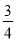 x+3,l2:y =-3x+3,若l2上一点M到l1的距离是1,试运用 “阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
x+3,l2:y =-3x+3,若l2上一点M到l1的距离是1,试运用 “阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
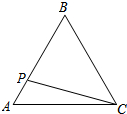 如图,等边△ABC边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC,则y关于x函数的图象大致为( )
如图,等边△ABC边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC,则y关于x函数的图象大致为( )| A. | 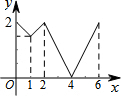 | B. | 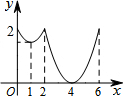 | C. | 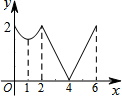 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
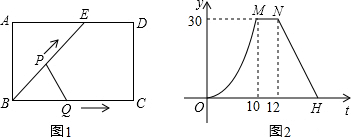 如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:
如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
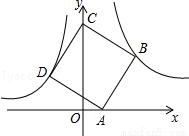
如图,点B(3,3)在双曲线y=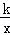 (x>0)上,点D在双曲线y=﹣
(x>0)上,点D在双曲线y=﹣ (x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(1)求k的值;
(2)求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 早晨,小刚沿着通往学校唯一的一条路(直线)上学,途中发现忘带盒饭,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
早晨,小刚沿着通往学校唯一的一条路(直线)上学,途中发现忘带盒饭,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com