
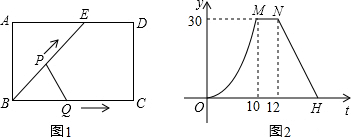
 如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:
如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.
解答 解:①根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,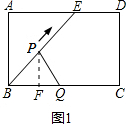
∴BC=BE=10cm,S△BCE=$\frac{1}{2}$BC•AB=30,
∴AB=6cm,故①正确;
①如图1,过点P作PF⊥BC于点F,
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=$\frac{AB}{BE}=\frac{4}{5}$,
∴PF=PBsin∠PBF=$\frac{4}{5}$t,
∴当0<t≤5时,y=$\frac{1}{2}$BQ•PF=$\frac{1}{2}$t•$\frac{4}{5}$t=$\frac{2}{5}$t2(故②正确);
③根据10-12秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=18,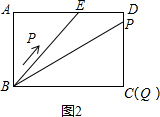
故点H的坐标为(18,0),
设直线NH的解析式为y=kx+b,
将点H(18,0),点N(12,30)代入可得:
$\left\{\begin{array}{l}{18k+b=0}\\{12k+b=30}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-5}\\{b=90}\end{array}\right.$.
故直线NH的解析式为:y=-5t+90,故③正确;
④如图2所示,sin∠PBQ=$\frac{1}{2}$时,∠PBQ=30°,
tan∠PBQ=$\frac{PQ}{BC}$=$\frac{18-t}{10}$=$\frac{\sqrt{3}}{3}$,
解得t=$\frac{54-10\sqrt{3}}{3}$,故④错误;
综上所述,错误的只有④,
故选:B.
点评 本题考查了二次函数的综合应用及动点问题的函数图象,根据图(2)判断出点P到达点E时,点Q到达点C是解题的关键,也是本题的突破口,难度较大


科目:初中数学 来源: 题型:解答题
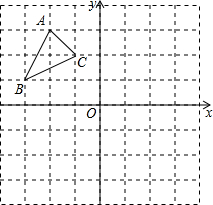 如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).
如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
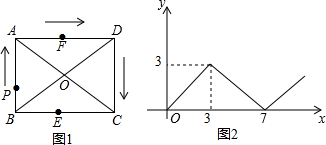 如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )| A. | 点C | B. | 点F | C. | 点D | D. | 点O |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
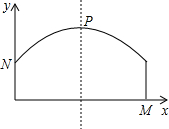 如图,某隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
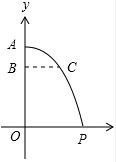 2008年7月某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口A,如图所示,如果空投物资离开A处后下落的垂直高度AB=160米时,它测A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为500米.
2008年7月某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口A,如图所示,如果空投物资离开A处后下落的垂直高度AB=160米时,它测A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为500米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
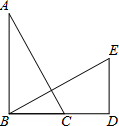 如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E
如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com