
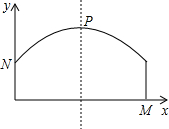
 如图,某隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.分析 (1)看图可得出M,P的坐标.
(2)已知M,P的坐标,易求出这条抛物线的函数解析式.
(2)将x=4代入(2)中的函数式求y的值,再与5m进行比较即可求解.
解答 解:(1)由题意得:
M(12,0),P(6,6),N(0,3);
(2)由顶点P(6,6)设此函数解析式为:y=a(x-6)2+6,
将点(0,3)代入得a=-$\frac{1}{12}$,
∴y=-$\frac{1}{12}$(x-6)2+6
=-$\frac{1}{12}$x2+x+3;
(3)当x=4时,代入y=-$\frac{1}{12}$x2+x+3=-$\frac{16}{12}$+7=$\frac{17}{3}$,
∵$\frac{17}{3}$>5,
∴能通过.
点评 本题考查了二次函数的应用:构建二次函数模型解决实际问题,利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:解答题
小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:


请根据图中给出的信息,解答下列问题:
(1)放入一个小球量筒中水面升高_______cm;
(2)求放入小球后量筒中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量筒中至少放入几个小球时有水溢出?
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
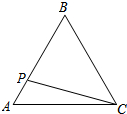 如图,等边△ABC边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC,则y关于x函数的图象大致为( )
如图,等边△ABC边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC,则y关于x函数的图象大致为( )| A. | 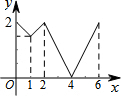 | B. | 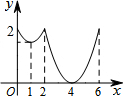 | C. | 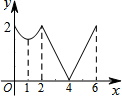 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
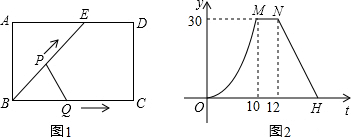 如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:
如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
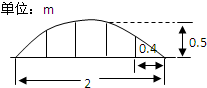 某学校院墙上部是由100段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔0.4m,加设一根不锈钢支柱,防护栏的最高点距护栏底部0.5m(如图),则这条护栏要不锈钢支柱总长度至少为( )
某学校院墙上部是由100段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔0.4m,加设一根不锈钢支柱,防护栏的最高点距护栏底部0.5m(如图),则这条护栏要不锈钢支柱总长度至少为( )| A. | 50m | B. | 100m | C. | 120m | D. | 160m |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
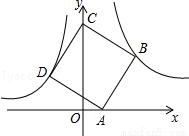
如图,点B(3,3)在双曲线y=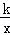 (x>0)上,点D在双曲线y=﹣
(x>0)上,点D在双曲线y=﹣ (x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(1)求k的值;
(2)求点A的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com