
| A. | 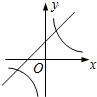 | B. | 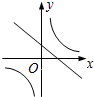 | C. | 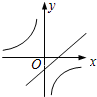 | D. | 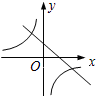 |
分析 分别根据一次函数和反比例函数图象的特点进行逐一分析即可,由于a的符号不确定,所以需分类讨论.
解答 解:A、由一次函数y=ax-a的图象y轴的正半轴相交可知-a>0,即a<0,与y=$\frac{a}{x}$(a≠0)的图象a>0相矛盾,故A选项错误;
B、由一次函数y=ax-a的图象y轴的正半轴相交可知-a>0,即a<0,与y=$\frac{a}{x}$(a≠0)的图象a>0相矛盾,故B选项错误;
C、由一次函数y=ax-a的图象与y轴的负半轴相交可知-a<0,即a>0,与y=$\frac{a}{x}$(a≠0)的图象a<0相矛盾,故C选项错误;
D、由一次函数y=ax-a的图象可知a<0,与y=$\frac{a}{x}$(a≠0)的图象a<0一致,故D选项正确.
故选:D.
点评 本题考查了一次函数的图象及反比例函数的图象,重点是注意y=k1x+b中k1、b及y=$\frac{{k}_{2}}{x}$中k2的取值.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
先化简,再求值:2(x+1)(x-1)-(2x-1)²其中x =-2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
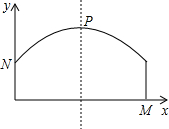 如图,某隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).把△ABC绕着原点O逆时针旋转90°得△A1B1C1,画出△A1B1C1,并写出C1的坐标.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).把△ABC绕着原点O逆时针旋转90°得△A1B1C1,画出△A1B1C1,并写出C1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
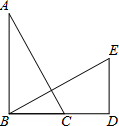 如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E
如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E查看答案和解析>>
科目:初中数学 来源: 题型:解答题
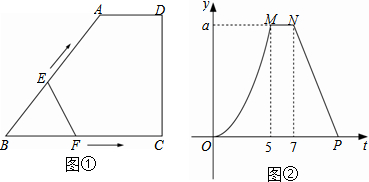
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
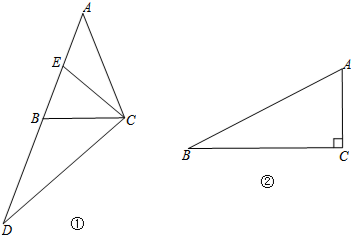
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com