
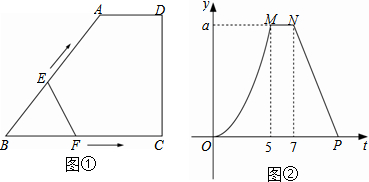
分析 (1)此题的关键是要理解分段函数的意义,OM段是曲线,说明E、F分别在BA、BC上运动,此时y、t的关系式是二次函数;MN段是线段,且平行于t轴,那么此时F运动到终点C,且E在线段AD上运动,此时y为定值;NP段是线段,此时y、t的函数关系式是一次函数,此时E在线段CD上运动,此时y值随t的增大而减小;根据上面的分析,可知在MN之间时,E在线段AD上运动,在这个区间E点运动了2秒,所以AD=2cm;根据OM段的函数图象知:当t=5时,E、F分别运动到A、C两点,那么AB=BC=5;
(2)利用待定系数法分别求两个解析式.
解答 解:(1)由图可知:OM段为抛物线,此时点E、F分别在BA、BC上运动;
当E、A重合,F、C重合时,t=5s,
∴AB=BC=5cm;故答案为:2,5;
(2)过A作AH⊥BC,H为垂足,由已知BH=3,BA=BC=5,
∴AH=4
∴当点E、F分别运动到A、C时△EBF的面积为:$\frac{1}{2}$×BC×AH=$\frac{1}{2}$×5×4=10,
即a的值为10,
点N所表示的实际意义:当点E运动7s时到达点D,此时点F沿BC已运动到点C
并停止运动,这时△EBF的面积为10 cm2;
(3)当点E在BA上运动时,设抛物线的解析式为y=at2,把M点的坐标(5,10)代入得a=$\frac{2}{5}$,
∴y=$\frac{2}{5}$t2,0<t≤5;
当点E在DC上运动时,设直线的解析式为y=kt+b,
把P(11,0),N(7,10)代入,得11k+b=0,7k+b=10,解得k=-$\frac{5}{2}$,b=$\frac{55}{2}$,
所以y=-$\frac{5}{2}$t+$\frac{55}{2}$,(7≤t<11)
把y=5分别代入y=$\frac{2}{5}$t2和y=-$\frac{5}{2}$t+$\frac{55}{2}$得,5=$\frac{2}{5}$t2和5=-$\frac{5}{2}$t+$\frac{55}{2}$,解得:t=$\frac{5\sqrt{2}}{2}$ 或t=9.
点评 此题主要考查了分段函数的应用、梯形的性质以及函数解析式的求法,能够正确的理解分段函数的意义是解答此题的关键.


科目:初中数学 来源: 题型:选择题
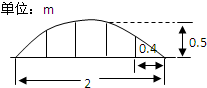 某学校院墙上部是由100段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔0.4m,加设一根不锈钢支柱,防护栏的最高点距护栏底部0.5m(如图),则这条护栏要不锈钢支柱总长度至少为( )
某学校院墙上部是由100段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔0.4m,加设一根不锈钢支柱,防护栏的最高点距护栏底部0.5m(如图),则这条护栏要不锈钢支柱总长度至少为( )| A. | 50m | B. | 100m | C. | 120m | D. | 160m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
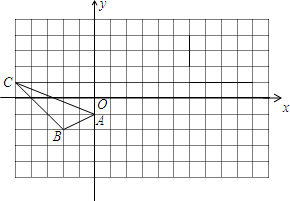 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
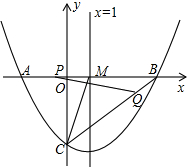 如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
对于二次函数y = x2-2mx-3,有下列结论:①它的图象与x轴有两个交点;②如果将它的图象向左平移3个单位 后过原点,则m=1;③如果当x = 2时的函数值与x = 8时的函数值相等,则m=5.其中一定正确的结论是____________.(把你认为正确结论的序号都填上)
后过原点,则m=1;③如果当x = 2时的函数值与x = 8时的函数值相等,则m=5.其中一定正确的结论是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com