
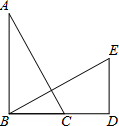
 如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E
如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E分析 (1)利用已知得出∠A=∠DBE,进而利用ASA得出△ABC≌△BDE即可;
(2)首先找出对应点,然后作对应点连线的垂直平分线,交点即为旋转中心;
(3)先求的OB的长,然后根据旋转的方向和旋转角的大小计算即可.
解答 解:证明(1)∵BE⊥AC
∴∠A+∠ABE=90°
∵∠ABC=90°
∴∠DBE+∠ABE=90°
∴∠A=∠DBE
在△ABC和△BDE中,$\left\{\begin{array}{l}{∠A=∠DBE}\\{BD=AB}\\{∠ABC=∠BDE=90}\end{array}\right.$,
∴△AOF≌△DOC.
(2)分别作对应点B、D连线的中垂线、A、B连线的垂直平分线,两线的交点即为旋转中心O.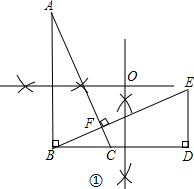
(3)如下图: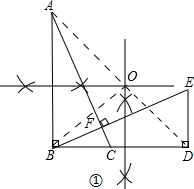
由作图可知,AO=BO=DO
∴∠OAB=∠OBA,∠OBD=∠ODB
∵∠OBA+∠OBD=90°
∴∠OAB+∠OBA+∠OBD+∠ODB=180°
∴A,O,D在同一直线上
∵AB=BD
∴△ABD为等腰直角三角形
∵O为AD的中点
∴∠BOD=90°.
在Rt△BOD中,$\frac{OB}{BD}=\frac{\sqrt{2}}{2}$,即:$\frac{OB}{2}=\frac{\sqrt{2}}{2}$,
∴OB=$\sqrt{2}$,
当△ABC按逆时针旋转时,点B经过的路径=$\frac{90}{360}×2πr=\frac{\sqrt{2}}{2}π$,
当△ABC按顺时针旋转时,点B经过的路径=$\frac{270}{360}×2πr=\frac{3\sqrt{2}}{2}π$.
∴B点所经过的路径长为$\frac{\sqrt{2}}{2}π$或$\frac{3\sqrt{2}}{2}π$..
点评 本题主要考查的是旋转的性质和全等三角形的判定,由旋转的性质确定出旋转中心和旋转半径以及旋转角的大小是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
认真阅读材料,然后回答问题:我们初中学习了多项式的运算法则,相应的我们可以计算出多项式的展开式,如:(a+b)1=a+b,
(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,…下面我们依次对(a+b)n展开式的各项系数进一步研究发现,当n取正整数是可以单独列成表中的形式: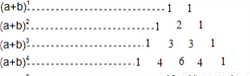
上面的多项式展开系数表称为“杨辉三角形”;仔细观察“杨辉三角形”,用你发现的规律回答下列问题:(1)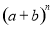 展开式中共有多少项?
展开式中共有多少项?
(2)请写出多项式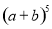 的展开式?
的展开式?
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
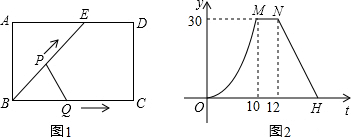 如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:
如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
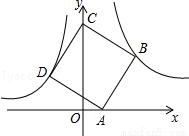
如图,点B(3,3)在双曲线y=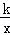 (x>0)上,点D在双曲线y=﹣
(x>0)上,点D在双曲线y=﹣ (x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(1)求k的值;
(2)求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
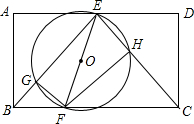 如图,矩形ABCD中,E为AD中点,点F为BC上的动点(不与B、C重合).连接EF,以EF为直径的圆分别交BE,CE于点G、H.设BF的长度为x,弦FG与FH的长度和为y,则下列图象中,能表示y与x之间的函数关系的图象大致是( )
如图,矩形ABCD中,E为AD中点,点F为BC上的动点(不与B、C重合).连接EF,以EF为直径的圆分别交BE,CE于点G、H.设BF的长度为x,弦FG与FH的长度和为y,则下列图象中,能表示y与x之间的函数关系的图象大致是( )| A. | 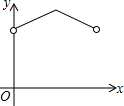 | B. | 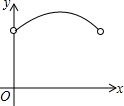 | C. | 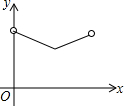 | D. | 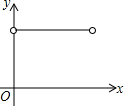 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 早晨,小刚沿着通往学校唯一的一条路(直线)上学,途中发现忘带盒饭,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
早晨,小刚沿着通往学校唯一的一条路(直线)上学,途中发现忘带盒饭,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com