练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．一次函数y=（3-m）x+m-5的图象经过第一，二，四象限，则m应为m＞5．

    分析 根据一次函数图象与系数的关系得到3-m＜0且m-5＞0，然后求出两部等式的公共部分即可．

    解答 解：根据题意得3-m＜0且m-5＞0，
    解得m＞5．
    故答案为：m＞5．

    点评 本题考查了一次函数图象与系数的关系：一次函数y=kx+b（k、b为常数，k≠0）是一条直线，当k＞0，图象经过第一、三象限，y随x的增大而增大；当k＜0，图象经过第二、四象限，y随x的增大而减小；图象与y轴的交点坐标为（0，b）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

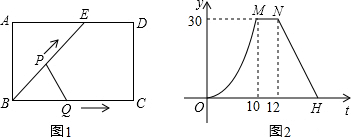    14．如图1，点E为矩形ABCD的边AD上一点，点P、点Q同时从点B出发，点P沿BE→ED→DC 运动到点C停止，点Q沿BC运动到点C停止，它们运动的速度都是1cm/s，设P、Q出发t秒时，△BPQ的面积为ycm2，已知y与t的函数关系如图2（曲线OM为抛物线的一部分），则下列结论：
    ①AB=6cm；
    ②当0＜t≤10时，y=$\frac{3}{10}$t2；
    ③NH所在直线的解析式为y=-5t+90；
    ④sin∠PBQ=$\frac{1}{2}$时，t=13秒．
    其中错误的结论个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

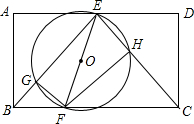    12．如图，矩形ABCD中，E为AD中点，点F为BC上的动点（不与B、C重合）．连接EF，以EF为直径的圆分别交BE，CE于点G、H．设BF的长度为x，弦FG与FH的长度和为y，则下列图象中，能表示y与x之间的函数关系的图象大致是（　　）
    A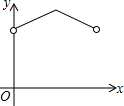．B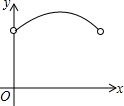．C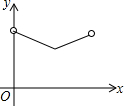．D．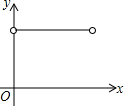

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．早晨，小刚沿着通往学校唯一的一条路（直线）上学，途中发现忘带盒饭，停下来往家里打电话，妈妈接到电话后带上饭盒马上赶往学校，同时小刚返回，两人相遇后，小刚立即赶往学校，妈妈回家，15分钟妈妈到家，再经过3分钟小刚到达学校，小刚始终以100米/分的速度步行，小刚和妈妈的距离y（单位：米）与小刚打完电话后的步行时间t（单位：分）之间的函数关系如图，下列四种说法：
    ①打电话时，小刚和妈妈的距离为1250米；
    ②小刚和妈妈相遇后，妈妈回家的速度为150米/分；
    ③打完电话后，经过23分钟小刚到达学校；
    ④小刚家与学校的距离为2550米．
    其中正确的个数是 （　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．解分式方程：$\frac{12}{{x}^{2}-9}$+$\frac{2}{3-x}$=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6，∠BDA=30°，求EF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知$\frac{a}{b}$=3，则$\frac{a-b}{b}$=2；分解因式：ab2-2ab+a=a（b-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）（π-2013）0+（$\frac{1}{3}$）-1-$\sqrt{4}$×|-3|
    （2）（$\sqrt{8}$+$\sqrt{3}$）×$\sqrt{6}$-（4$\sqrt{2}$-3$\sqrt{6}$）÷2$\sqrt{2}$
    （3）$\sqrt{8}$+2$\sqrt{3}$-（$\sqrt{27}$-$\sqrt{2}$）
    （4）（$\sqrt{2}$-$\sqrt{3}$）2+2$\sqrt{\frac{1}{3}}$×3$\sqrt{2}$
    （5）$\sqrt{12}$+（$\sqrt{2}$+1）（$\sqrt{2}$-1）+$\sqrt{2}$×$\sqrt{18}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列说法中，真命题的个数是（　　）
    ①有两边对应相等的两个直角三角形全等；
    ②一锐角和一条边对应相等的两个直角三角形全等；
    ③两个锐角对应相等的两个直角三角形全等．
    A．1个B．2 个C．3个D．0个

    查看答案和解析>>

    同步练习册答案